

分析 执行程序框图,写出每次循环得到的S,n,k的值,观察数列{an}的前n项和的变化规律,即可求解.利用裂项法即可求和.
解答 解:执行程序框图,有
S=0.n=2,k=1
不满足k≤10第1次执行循环体,S=$\frac{1}{2}$,n=4,k=2
不满足k≤10第2次执行循环体,S=$\frac{1}{2}$+$\frac{1}{4}$,n=6,k=3
不满足k≤10第3次执行循环体,S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$,n=8,k=4
不满足k≤10第3次执行循环体,S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{8}$,n=10,k=5
…
综上可知,程序框图的功能是求一个数列{an}的前10项和,S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{8}$+…+$\frac{1}{20}$
故数列{an}的一个通项公式an=$\frac{1}{2n}$.
则an•an+1=$\frac{1}{2n}•\frac{1}{2(n+1)}$=$\frac{1}{4}$($\frac{1}{n}$-$\frac{1}{n+1}$),
则数列{an•an+1}的前2016项和S=$\frac{1}{4}$(1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$)=$\frac{1}{4}$(1-$\frac{1}{2017}$)=$\frac{1}{4}×\frac{2016}{2017}$=$\frac{504}{2017}$
故答案为:$\frac{1}{2n}$,$\frac{504}{2017}$.
点评 本题主要考察了程序框图和算法,数列通项公式和和的求法,根据程序框图求出通项公式以及利用裂项法进行求和是解决本题的关键.


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | [-1,2) | C. | (2,+∞) | D. | (-∞,-1]∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{40}{9}$ | B. | $-\frac{8}{21}$ | C. | 1 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 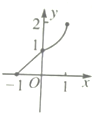 | B. | 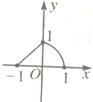 | C. | 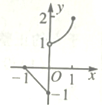 | D. | 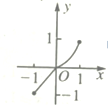 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{{x}^{2}}$,g(x)=($\sqrt{x}$)2 | B. | f(x)=1,g(x)=x0 | ||
| C. | f(x)=$\left\{\begin{array}{l}{x,x≥0}\\{-x,x<0}\end{array}\right.$,g(x)=$\sqrt{{x}^{2}}$ | D. | f(x)=x+1,g(x)=$\frac{{x}^{2}-1}{x-1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com