
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() ,点E在BC上,
,点E在BC上,![]() .
.
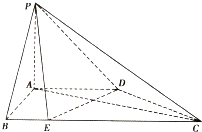
(1)求证:平面![]() 平面PAC;
平面PAC;
(2)若直线PE与平面PAC所成的角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
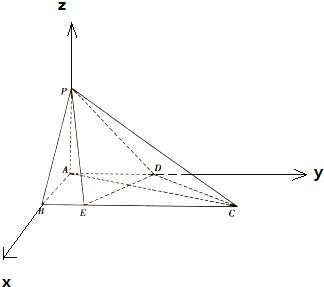
(1)以A为原点,AB、AD、AP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能证明平面PED⊥平面PAC.
(2)求出平面PAC的一个法向量和平面PCD的一个法向量,利用向量法能求出二面角A﹣PC﹣D的余弦值.
证明:(1)∵平面PAB⊥平面ABCD,
平面PAB∩平面ABCD=AB,PA⊥AB,
∴PA⊥平面ABCD,
∵AB⊥AD,∴以A为原点,AB、AD、AP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,
则A(0,0,0),D(0,2,0),E(2,1,0),C(2,4,0),设P(0,0,λ),λ>0,
则![]() (2,4,0),
(2,4,0),![]() (0,0,﹣2),
(0,0,﹣2),![]() (2,﹣1,0),
(2,﹣1,0),
∴![]() 4﹣4+0=0,
4﹣4+0=0,![]() 0,
0,
∴DE⊥AC,DE⊥AP,
∵AC∩AP=A,∴DE⊥平面PAC,
∵DE平面PED,∴平面PED⊥平面PAC.
解:(2)由(1)知平面PAC的一个法向量为
![]() (2,﹣1,0),
(2,﹣1,0),
∵直线PE与平面PAC所成的角的正弦值为![]() ,
,
![]() (2,1,﹣λ),
(2,1,﹣λ),
∴|cos![]() |=|
|=|![]() |
|![]() ,
,
解得λ=±2,
∵λ>0,∴λ=2,即P(0,0,2),
设平面PCD的一个法向量为![]() (x,y,z),
(x,y,z),
![]() (2,2,0),
(2,2,0),![]() (0,﹣2,2),
(0,﹣2,2),
∴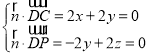 ,取x=1,得
,取x=1,得![]() (1,﹣1,﹣1),
(1,﹣1,﹣1),
∴cos![]() ,
,
∵二面角A﹣PC﹣D的平面角是锐角,
∴二面角A﹣PC﹣D的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,
,![]() 分别为椭圆C:
分别为椭圆C:![]() 的左右焦点,椭圆
的左右焦点,椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆C上,不在
在椭圆C上,不在![]() 轴上的动点P与动点Q关于原点O对称,且四边形
轴上的动点P与动点Q关于原点O对称,且四边形![]() 的周长为
的周长为![]() .
.
(1)求动点P的轨迹方程;
(2)在动点P的轨迹上有两个不同的点M![]() ,N
,N![]() ,线段MN的中点为G,已知点
,线段MN的中点为G,已知点![]() 在圆
在圆![]() 上,求
上,求![]() 的最大值,并判断此时ΔOMN的形状.
的最大值,并判断此时ΔOMN的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
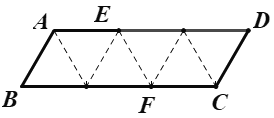
【题目】如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的表面积为__________;若该六面体内有一小球,则小球的最大体积为___________.
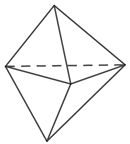
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两种理财产品![]() 和
和![]() ,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
注:![]() ,
,![]()
(1)若甲、乙两人分别选择了产品![]() 投资,一年后他们中至少有一人获利的概率大于
投资,一年后他们中至少有一人获利的概率大于![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若丙要将20万元人民币投资其中一种产品,以一年后的投资收益的期望值为决策依据,则丙选择哪种产品投资较为理想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三4班有50名学生进行了一场投篮测试,其中男生30人,女生20人.为了了解其投篮成绩,甲、乙两人分别都对全班的学生进行编号(1-50号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮测试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:
甲抽取的样本数据
编号 | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 | 47 |
性别 | 男 | 女 | 男 | 男 | 女 | 男 | 女 | 男 | 女 | 女 |
投篮成 绩 | 90 | 60 | 75 | 80 | 83 | 85 | 75 | 80 | 70 | 60 |
乙抽取的样本数据
编号 | 1 | 8 | 10 | 20 | 23 | 28 | 33 | 35 | 43 | 48 |
性别 | 男 | 男 | 男 | 男 | 男 | 男 | 女 | 女 | 女 | 女 |
投篮成 绩 | 95 | 85 | 85 | 70 | 70 | 80 | 60 | 65 | 70 | 60 |
(Ⅰ)在乙抽取的样本中任取3人,记投篮优秀的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?
优秀 | 非优秀 | 合计 | |
男 | |||
女 | |||
合计 | 10 |
(Ⅲ)判断甲、乙各用何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优?说明理由.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式: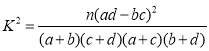 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:![]() ):男生成绩在175
):男生成绩在175![]() 以上(包括175
以上(包括175![]() )定义为“合格”,成绩在175
)定义为“合格”,成绩在175![]() 以下(不包括175
以下(不包括175![]() )定义为“不合格”.女生成绩在165
)定义为“不合格”.女生成绩在165![]() 以上(包括165
以上(包括165![]() )定义为“合格”,成绩在165
)定义为“合格”,成绩在165![]() 以下(不包括165
以下(不包括165![]() )定义为“不合格”.
)定义为“不合格”.
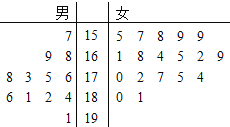
(1)求五年一班的女生立定跳远成绩的中位数;
(2)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(3)若从五年一班成绩“合格”的学生中选取2人参加复试,用![]() 表示其中男生的人数,写出
表示其中男生的人数,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com