
【题目】已知函数![]() ,令
,令![]() ,其中
,其中![]() 是函数
是函数![]() 的导函数.
的导函数.
(Ⅰ)当![]() 时,求
时,求![]() 的极值;
的极值;
(Ⅱ)当![]() 时,若存在
时,若存在![]() ,使得
,使得![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) 极小值![]() ,无极大值;(Ⅱ)
,无极大值;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)把![]() 代入函数
代入函数![]() 的解析式,求其导函数,由导函数的零点对定义域分段,得到函
的解析式,求其导函数,由导函数的零点对定义域分段,得到函
数在各区间段内的单调性,从而求得函数极值;(Ⅱ)由函数的导函数可得函数的单调性,求得函数在![]() 上的最值,再由
上的最值,再由![]() 恒成立,结合分离参数可得
恒成立,结合分离参数可得![]() ,构造函数
,构造函数![]() ,利用导数求其最值得
,利用导数求其最值得![]() 的范围.
的范围.
试题解析:(Ⅰ)依题意![]() ,则
,则![]()
当a=0时,![]()
令![]() 解得
解得![]() ;
;
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以![]() 的单调递减区间为(0,
的单调递减区间为(0,![]() ),单调递增区间为(
),单调递增区间为(![]() ,+∞)
,+∞)
所以![]() 时
时![]() 取得极小值
取得极小值![]() ,无极大值.
,无极大值.
(Ⅱ)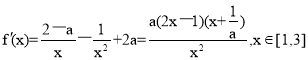
当![]() 即
即![]() 时,恒有
时,恒有![]() 成立,
成立,
所以![]() 在[1,3]上是单调递减.
在[1,3]上是单调递减.
所以![]()
所以![]() ,
,
因为存在![]() ,使得
,使得![]() 恒成立,
恒成立,
所以![]() 整理得
整理得
![]()
又![]() <0,所以
<0,所以![]()
令![]() =-
=-![]() ,则
,则![]() ∈(2,8),构造函数
∈(2,8),构造函数![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,此时函数单调递增,
,此时函数单调递增,
当![]() 时,
时,![]() ,此时函数单调递减,
,此时函数单调递减,
所以![]() ,
,
所以m的取值范围为(![]() ,+∞).
,+∞).


科目:高中数学 来源: 题型:
【题目】(1)已知函数f(x)(x∈R)是奇函数,且当x>0时,f(x)=2x-1,求函数f(x)的解析式.
(2)已知x+y=12,xy=9且x<y,求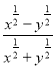 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合P={x|a+1≤x≤2a+1},Q={x|1≤2x+5≤15}.
(1)已知a=3,求(RP)∩Q;
(2)若P∪Q=Q,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的动点,且满足
两侧的动点,且满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
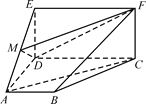
【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,![]() ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第![]() 届夏季奥林匹克运动会将于 2016 年 8 月 5 日—21 日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据( 单位: 枚).
届夏季奥林匹克运动会将于 2016 年 8 月 5 日—21 日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据( 单位: 枚).
第 | 第 | 第 | 第 | 第 | |
中国 |
|
|
|
|
|
俄罗斯 |
|
|
|
|
|
(1)根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图, 并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度( 不要求计算出具体数值, 给出结论即可);
(2)甲、 乙、 丙三人竞猜今年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多( 假设两国代表团获得的金牌数不会相等) , 规定甲、 乙、 丙必须在两个代表团中选一个, 已知甲、 乙猜中国代表团的概率都为![]() , 丙猜中国代表团的概率为
, 丙猜中国代表团的概率为![]() , 三人各自猜哪个代表团的结果互不影响.现让甲、 乙、 丙各猜一次, 设三人中猜中国代表团的人数为
, 三人各自猜哪个代表团的结果互不影响.现让甲、 乙、 丙各猜一次, 设三人中猜中国代表团的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com