
����Ŀ�������ڼ䣬�����н�Լ�������˷ѡ�֮����Ȼ������ij��ͨ�����ѯ��100���Ա�ͬ�ľ����Ƿ������������̡��ж����õ����µ���������
�����������̡� | �����������̡� | |
�� | 45 | 10 |
Ů | 30 | 15 |
P��K2��k�� | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 5.024 |
���� ![]()
���ո������õ�����ȷ�����ǣ� ��
A.�ڷ�����ĸ��ʲ�����l%��ǰ���£���Ϊ�����о����ܷ����������̡����Ա��йء�
B.�ڷ�����ĸ��ʲ�����l%��ǰ���£���Ϊ�����о����ܷ����������̡����Ա��ء�
C.��90%���ϵİ�����Ϊ�����о����ܷ����������̡����Ա��йء�
D.��90%���ϵİ�����Ϊ�����о����ܷ����������̡����Ա��ء�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪y=ax2+bx��a��0��ͨ���㣨1��2��������ͼ����y=��x2+2x��ͼ���ж������㣨��ͼ��ʾ���� 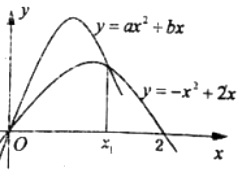
��1����y=ax2+bx��y=��x2+2x��Χ�ɵ����S��a�ĺ�����ϵ��
��2����a��bΪ��ֵʱ��Sȡ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
��
����![]() ʱ������
ʱ������![]() �ĵ������䣻
�ĵ������䣻
����������![]() �ڵ�
�ڵ�![]() ��������
��������![]() ������
������![]() ���ڵ�
���ڵ�![]() ����
����![]() ��ֵ��
��ֵ��
������![]() ���������
���������![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
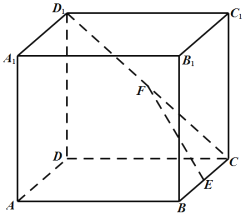
����Ŀ����ͼ����������![]() �У�
�У� ![]() �ֱ����߶�
�ֱ����߶�![]() ���е㣮
���е㣮
��1��������ֱ��![]() ��
��![]() ���ɽǵĴ�С��
���ɽǵĴ�С��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵĴ�С��
���ɽǵĴ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ�����Ϊ![]() �ĺ���
���![]() �������������
�������������![]() ��
��![]() ����ͬʱ���㣺
����ͬʱ���㣺
��![]() ��
��![]() ���ǵ����������ڵ���������
���ǵ����������ڵ���������![]() ʱ��
ʱ�� ![]() ��ֵ��Ҳ��
��ֵ��Ҳ��![]() ��
��
��ƺ���![]() ������
������![]() �ϵġ���ֵ��������
�ϵġ���ֵ��������
��1����֤������![]() ���Ƕ�����
���Ƕ�����![]() �ϵġ���ֵ��������
�ϵġ���ֵ��������
��2����֪![]() ��
��![]() ��������
��������![]() �ϵġ���ֵ����������
�ϵġ���ֵ����������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ��x+2����x��1����0�Ľ⼯Ϊ�� ��
A.{x|x����2��x��1}
B.{x|��2��x��1}
C.{x|x����1��x��2}
D.{x|��1��x��2}
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��������x1 �� x2��R��x1��x2 �� ʹ��f��x1��=f��x2����������ʵ��a��ȡֵ��Χ�� ��
��������x1 �� x2��R��x1��x2 �� ʹ��f��x1��=f��x2����������ʵ��a��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѡ���⡿��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣����������ָ�����������𣮽��Ӧд������˵����֤�����̻����㲽�裮
A��ѡ��4��1������֤��ѡ��
��ͼ����ABC�Ķ���A��C��ԲO�ϣ�B��Բ�⣬�߶�AB��ԲO���ڵ�M��

��1����BC��ԲO�����ߣ���AB��8��BC��4�����߶�AM�ij��ȣ�
��2�����߶�BC��ԲO������һ��N����AB��2AC����֤��BN��2MN��
B��ѡ��4��2��������任
��a��b��R����ֱ��l��ax��y��7��0�ھ���A= ![]() ��Ӧ�ı任�����£��õ���ֱ��Ϊl����9x��y��91��0����ʵ��a��b��ֵ��
��Ӧ�ı任�����£��õ���ֱ��Ϊl����9x��y��91��0����ʵ��a��b��ֵ��
C��ѡ��4��4������ϵ���������
��ƽ��ֱ������ϵxOy�У�ֱ��l��  (tΪ����)��������C��
(tΪ����)��������C��  (kΪ����)����A��B���㣬���߶�AB�ij���
(kΪ����)����A��B���㣬���߶�AB�ij���
D��ѡ��4��5������ʽѡ��
��a��b����֤��a4��6a2b2��b4��4ab(a2��b2)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ a��0 �� a��1��������f��x��=loga��x��1����g��x��=loga��5��x����
��1������h��x��=f��x����g��x���Ķ�����
��2�����۲���ʽf��x����g��x������ʱx��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com