
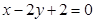 经过椭圆
经过椭圆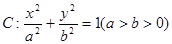 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆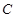 的右顶点为
的右顶点为 ,点
,点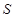 是椭圆
是椭圆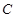 上位于
上位于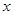 轴上方的动点,直线
轴上方的动点,直线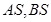 与直线
与直线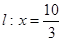 分别交于
分别交于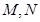 两点。
两点。
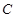 的方程;
的方程;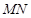 的长度的最小值;
的长度的最小值;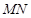 的长度最小时,在椭圆
的长度最小时,在椭圆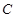 上是否存在这样的点
上是否存在这样的点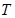 ,使得
,使得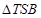 的面积为
的面积为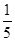 ?若存在,确定点
?若存在,确定点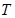 的个数,若不存在,说明理由。
的个数,若不存在,说明理由。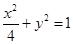 ;(Ⅱ)
;(Ⅱ)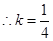 时,线段
时,线段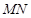 的长度取最小值
的长度取最小值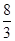
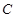 上存在2个不同的点
上存在2个不同的点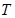 ,使得
,使得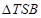 的面积为
的面积为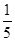
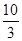 ,
,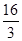 k).由题设条件可以求出N(
k).由题设条件可以求出N(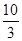 ,-
,-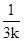 ),所以|MN|得到表示,再由均值不等式进行求解
),所以|MN|得到表示,再由均值不等式进行求解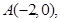
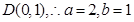 ;故椭圆
;故椭圆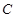 的方程为
的方程为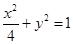
 显然存在,且
显然存在,且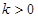 ,故可设直线
,故可设直线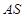 的方程为
的方程为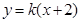 ,从而
,从而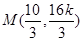
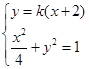 得
得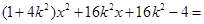 0
0 则
则 得
得 ,
,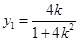 即
即 又
又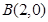
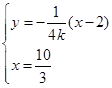 得
得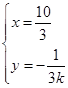
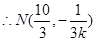 故
故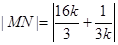
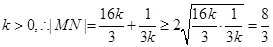
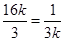 ,即
,即 时等号成立。
时等号成立。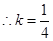 时,线段
时,线段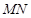 的长度取最小值
的长度取最小值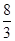
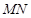 取最小值时,
取最小值时,
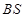 的方程为
的方程为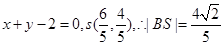
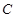 上存在点
上存在点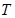 ,使得
,使得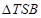 的面积等于
的面积等于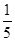 ,只须
,只须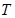 到直线
到直线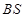 的距离等于
的距离等于 ,所以
,所以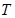 在平行于
在平行于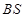 且与
且与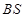 距离等于
距离等于 的直线
的直线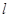 上。设直线
上。设直线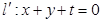
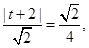 解得
解得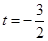 或
或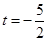
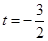 时,
时, 得
得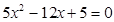 ,
, ,故有2个不同的交点;
,故有2个不同的交点;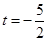 时,
时, 得
得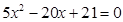 ,
,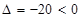 ,故没有交点;
,故没有交点;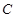 上存在2个不同的点
上存在2个不同的点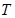 ,使得
,使得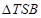 的面积为
的面积为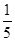


科目:高中数学 来源:不详 题型:解答题
 :
: 的两个焦点为
的两个焦点为 ,点
,点 在椭圆
在椭圆 上,且
上,且 .
. 的方程;
的方程; 过圆
过圆 的圆心,交椭圆
的圆心,交椭圆 于
于 两点,且
两点,且 关于点
关于点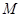 对称,求直线
对称,求直线 的方程。
的方程。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的焦点,离心率是
的焦点,离心率是
 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com