Question

【题目】已知是定义在上的偶函数，且满足，若当时，，则函数在区间上零点的个数为（ ）

A. 2017 B. 2018 C. 4034 D. 4036

Answer 1

【答案】D

【解析】试题分析：函数g（x）=f（x）﹣e﹣|x|在区间[﹣2018，2018]上零点的个数函数的图象与y=e﹣|x|的图象交点个数．是定义在上的偶函数，由得f（x）是周期为2的偶函数，根据当x∈[0，1]时，，作出y=f（x）与图象,结合图象即可．

详解：函数g（x）=f（x）﹣e﹣|x|在区间[﹣2018，2018]上零点的个数函数的图象与y=e﹣|x|的图象交点个数．

由是定义在上的偶函数，且满足，即f（﹣x）=f（x）．

又∵，f（x）是周期为2的偶函数．

∵当x∈[0，1]时，，

作出y=f（x）与图象如下图，

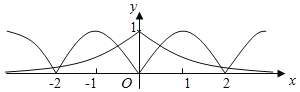
可知每个周期内有两个交点，所以函数g（x）=f（x）﹣e﹣|x|在区间[﹣2018，2018]上零点的个数为2018×2=4036．

故选：D．