
【题目】如图所示,在△ABC中,![]() ,AD是∠BAC的平分线,且
,AD是∠BAC的平分线,且![]() .
.

(1)求k的取值范围;
(2)若![]() ,求k为何值时,BC最短.
,求k为何值时,BC最短.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)(方法一)利用正弦定理在△ABC和△ACD中分别建立等式,通过整理便可得到k关于角的关系式;
(方法二)AD将△ABC一分为二,即以AD为界将△ABC分成两个三角形,通过面积相等建立等式;
(方法三)利用余弦定理在△ABC和△ACD中分别建立等式,通过整理便可得到k关于角的关系式;
(2)在![]() ,由余弦定理可得
,由余弦定理可得![]() ,根据三角形面积公式可得
,根据三角形面积公式可得![]() ,则
,则![]() ,记
,记![]() ,则
,则![]() ,可整理为
,可整理为![]() ,进而求得满足最值的条件即可
,进而求得满足最值的条件即可
(1)方法一:由AD是∠BAC的平分线,可得![]() ,则
,则![]() ,
,
在△ABC中,由正弦定理得![]() ①,
①,
在△ACD中,由正弦定理得 ②,
②,
由①②得 ,
,
又![]() ,
,![]() ,
,
所以![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]()
方法二:由![]() ,
,
得![]()
![]() ,
,
又![]() ,
,![]() ,整理得
,整理得![]() ,
,
因为![]() ,所以
,所以![]()
方法三:在△ADC中,![]() ,
,
在△ABD中,![]() ,
,
又![]() ,则
,则![]()
![]() ,
,
解得![]() ,
,
因为![]() ,所以
,所以![]()
(2)由余弦定理得![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
故![]() ,
,
记![]() ,则
,则![]() ,
,
![]() (其中
(其中![]() ),
),
故当![]() 时,y取得最小值3,此时
时,y取得最小值3,此时![]() ,
,
又由(1)知![]() ,
,
而![]() ,
,
则![]() ,故
,故![]() ,
,
即当![]() 时,BC最短
时,BC最短


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在![]() .
.
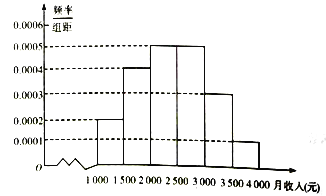
(1)求居民收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数、平均数及其众数;
(3)为了分析居民的收入与年龄、职业等方面的关系,从这10000人中用分层抽样方法抽出100人作进一步分析,则应月收入为![]() 的人中抽取多少人?
的人中抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请解决下列问题:
(1)设圆柱的底面半径为![]() ,母线长为
,母线长为![]() ,写出圆柱的表面积计算公式;
,写出圆柱的表面积计算公式;
(2)设圆锥的底面半径为![]() ,母线长为
,母线长为![]() ,写出圆锥的表面积计算公式;
,写出圆锥的表面积计算公式;
(3)设圆台的上、下底面半径分别为![]() 、
、![]() ,母线长为
,母线长为![]() ,写出圆台的表面积计算公式;
,写出圆台的表面积计算公式;
(4)写出上述![]() 个表面积计算公式之间的关系.
个表面积计算公式之间的关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2-(2m+1)x+m.
(1)若方程f(x)=0有两个不等的实根x1,x2,且-1<x1<0<x2<1,求m的取值范围;
(2)若对任意的x∈[1,2],![]() ≤2恒成立,求m的取值范围.
≤2恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形ABCD中, AB=2,BD=![]() ,AB⊥BC,∠BCD=2∠ABD,△ABD的面积为2.
,AB⊥BC,∠BCD=2∠ABD,△ABD的面积为2.

(1)求AD的长;
(2)求△CBD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() .
.
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求与直线![]() 平行,且被曲线
平行,且被曲线![]() 截得的弦长为
截得的弦长为![]() 的直线
的直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() 且
且![]() ,点
,点![]() 分别是棱
分别是棱![]() 的中点,将四边形
的中点,将四边形![]() 沿着
沿着![]() 转动,使得
转动,使得![]() 与
与![]() 重合,形成如图所示多面体,分别取
重合,形成如图所示多面体,分别取![]() 的中点
的中点![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,求
,求![]() 与平面
与平面![]() 所成的正弦值.
所成的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com