练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线为参数），以坐标原点为极点，轴为极轴建立极坐标系，曲线．

    （1）求曲线的直角坐标方程和直线的普通方程；

    （2）求与直线平行，且被曲线截得的弦长为的直线的方程．

    【答案】（1）C：x2+（y-1）2=1，x+y-3=0；（2）或

    【解析】

    （1）对直线的参数方程进行消参，得到普通方程；利用把曲线的极坐标方程，转化为直角坐标方程.
    （2）根据圆的半径和弦长，求出弦心距，再由两平行线间的距离，得到直线的方程.

    （1）直线 （为参数），转换为直角坐标方程为：．

    曲线．转换为直角坐标方程为：．

    转换为标准式为

    （2）曲线为圆，半径为1，弦长为，

    所以圆心到直线的距离

    设与直线平行的直线方程为：

    则：圆心到直线的距离，

    解得：，

    直线的方程为：或．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中，，为棱的中点，.

    （1）证明：平面；

    （2）设二面角的正切值为，，，求异面直线与所成角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在△ABC中，，AD是∠BAC的平分线，且.

    （1）求k的取值范围；

    （2）若，求k为何值时，BC最短.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为考查某种疫苗预防疾病的效果，进行动物实验，得到统计数据如下：

    未发病

    发病

    总计

    未注射疫苗

    20

    注射疫苗

    30

    总计

    50

    50

    100

    现从所有试验动物中任取一只，取到“注射疫苗”动物的概率为.

    （1）求列联表中的数据，，，的值；

    （2）判断疫苗是否有效？

    （3）能够有多大把握认为疫苗有效？

    （参考公式，）

    0.05

    0.01

    0.005

    0.001

    3.841

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数f（x）满足条件f（0）＝1，及f（x+1）﹣f（x）＝2x．

    （1）求函数f（x）的解析式；

    （2）在区间[﹣1，1]上，y＝f（x）的图象恒在y＝2x+m的图象上方，试确定实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆过点，若点与椭圆左焦点构成的直线的斜率为与右焦点构成的直线的斜率为，且;

    （1）求椭圆的方程；

    （2）过点的直线与椭圆的另一个交点为与轴的交点为，为椭圆的中心，点在椭圆上，且，若,求直线的方程

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论函数的单调性；

    （2）设，若对任意给定的，关于的方程在上有两个不同的实数根，求实数的取值范围（其中为自然对数的底数）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

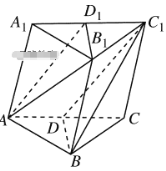
    【题目】如图所示，在斜三棱柱ABC—A1B1C1中，点D，D1分别为AC，A1C1上的点．

    (1)当的值等于何值时，BC1∥平面AB1D1；

    (2)若平面BC1D∥平面AB1D1，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，，，为的中点．

    （1）求证：平面；

    （2）在线段上是否存在一点，使得平面平面？若存在，证明你的结论，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案