
| A. | 130 | B. | 132 | C. | 134 | D. | 136 |
分析 an+1+(-1)n an=2n-1,可得a2-a1=1,a3+a2=3,a4-a3=5,a5+a4=7,a6-a5=9,a7+a6=11,…a16-a15=29.
从而可得a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,a9+a11=2,a12+a10=40,a13+a15=2,a16+a14=56,即可得出.
解答 解:∵an+1+(-1)n an=2n-1,
∴a2-a1=1,a3+a2=3,a4-a3=5,a5+a4=7,a6-a5=9,a7+a6=11,…a16-a15=29.
从而可得a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,a9+a11=2,a12+a10=40,a13+a15=2,a16+a14=56,
从第一项开始,依次取2个相邻奇数项的和都等于2,从第二项开始,
依次取2个相邻偶数项的和构成以8为首项,以16为公差的等差数列.
∴{an}的前16项和为 4×2+8×4+$\frac{4×3}{2}×16$=136.
故选:D.
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{2}$ | B. | $\frac{5π}{4}$ | C. | $\frac{3+π}{2}$ | D. | 3+π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
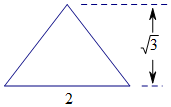 一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )
一个四棱锥的侧棱长都相等,底面是正方形,且其正视图为如图所示的等腰三角形,则该四棱锥的体积是( )| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com