
分析 (Ⅰ)利用两个向量的数量积的定义,正弦函数的周期性求得ω,再根据函数的图象经过点M,求得函数f(x)的解析式.
(Ⅱ)依题意利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再利用正弦函数的奇偶性,求得m的最小值.
解答 解:(Ⅰ)$f(x)=(\overrightarrow a+\overrightarrow b)(\overrightarrow a-\overrightarrow b)={\overrightarrow a^2}-{\overrightarrow b^2}$=sin2(ωx+φ)+4-1-cos2(ωx+φ)=-cos(2ωx+2φ)+3,
由题可知,$\frac{T}{4}=1$,∴T=4,∴由$T=\frac{2π}{2ω}=4$得$ω=\frac{π}{4}$.
又∵函数f(x)经过点$M(1,\frac{7}{2})$,∴$-cos(\frac{π}{2}•1+2φ)+3=\frac{7}{2}$,∴$cos(\frac{π}{2}+2φ)=-\frac{1}{2}$,
∵$0<φ<\frac{π}{4}$,∴$\frac{π}{2}+2φ=\frac{2π}{3}$,即$φ=\frac{π}{12}$,
∴函数f(x)的解析式为f(x)=$-cos(\frac{π}{2}x+\frac{π}{6})+3$.
(Ⅱ)先将函数y=f(x)=-cos($\frac{π}{2}$x+$\frac{π}{6}$)+3图象上各点的横坐标变为原来的π倍,纵坐标不变,
可得y=-cos($\frac{1}{2}$x+$\frac{π}{6}$)+3的图象;
再向右平移m(m>0)个单位长度,向下平移3个单位长度,得到函数y=$g(x)=-cos({\frac{1}{2}(x-m)+\frac{π}{6}})$
=$-cos(\frac{1}{2}x-\frac{1}{2}m+\frac{π}{6})$ 的图象.
∵函数g(x)关于原点对称,∴函数g(x)为奇函数,即$-\frac{1}{2}m+\frac{π}{6}=kπ+\frac{π}{2}(k∈Z)$,
∴$m=-2kπ-\frac{2π}{3}(k∈Z)$,
∵m>0,∴当k=-1时,m的最小值为$\frac{4π}{3}$,
∴综上所述,实数m的最小值为$\frac{4π}{3}$.
点评 本题主要考查两个向量的数量积的定义,正弦函数的周期性、奇偶性,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1) | B. | [0,2] | C. | [-2,2) | D. | [-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 130 | B. | 132 | C. | 134 | D. | 136 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
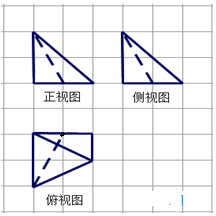 如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线和虚线画出的是某空间几何体的三视图,则该几何体的体积为( )| A. | 2 | B. | $\frac{2}{3}$ | C. | 4 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )| A. | $4+\frac{2π}{3}$ | B. | $4+\frac{{\sqrt{2}π}}{6}$ | C. | $12+\frac{2π}{3}$ | D. | $12+\frac{{\sqrt{2}π}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com