练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．若函数f（x）=（$\frac{1}{2}$）x，g（x）=|log3（x-1）|，则方程f（x）-g（x）=0的实根个数为（　　）
    A．3B．2C．1D．0

    分析 利用两个函数的图象判断交点个数即可．

    解答 解：在同一个坐标系中画出两个函数f（x）=（$\frac{1}{2}$）x，g（x）=|log3（x-1）|的图象，如图：
    可知两个函数的图象有2个交点，
    则方程f（x）-g（x）=0的实根个数为2．
    故选：B．

    点评 本题考查函数的图象的应用，零点个数的判断，考查数形结合思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．（x+$\frac{2}{\sqrt{x}}$）6的展开式中，x3项的系数是60（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=ex-ax2-2x（a∈R）．
    （1）当a=0时，求f（x）的最小值；
    （2）当a＜$\frac{e}{2}$-1时，证明：不等式f（x）＞$\frac{e}{2}$-1在（0，+∞）上恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知x，y是[0，1]上的两个随机数，则x，y满足y＞2x的概率为（　　）
    A．$\frac{1}{4}$B．$\frac{1}{2}$C．$\frac{3}{4}$D．$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．设等比数列{an}的公比为q，前n项和为Sn，则“q=1”是“S6=3S2”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

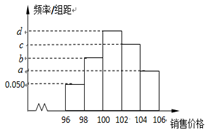    7．某企业市场调研部为调查新开发的产品定价与销量之间的关系，在某地区进行小范围差价试销，已知该产品定价区间为[96，106]（单位：元/件），已知统计了600件产品的销售价格，其频率分布直方图如图所示，若各个小方形的高构成一个等差数列，则在这600件产品中，销售价格在区间[98，102）内的产品件数是135．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知cos（x-$\frac{π}{3}$）=$\frac{1}{3}$，则cos（2x-$\frac{5π}{3}$）+sin2（$\frac{π}{3}$-x）的值为（　　）
    A．-$\frac{1}{9}$B．$\frac{1}{9}$C．$\frac{5}{3}$D．-$\frac{5}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数f（x）=|lnx|，$g（x）=\left\{\begin{array}{l}0，0＜x≤1\\|{x^2}-4|-2，x＞1\end{array}\right.$若方程|f（x）+g（x）|=a有4个实根，则a的取值范围是（　　）
    A．（0，1]B．（0，2-ln2）C．[1，2-ln2]D．[1，2-ln2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．角α的终边经过的一点P的坐标是（-$\sqrt{3}$，a），则“|a|=1”的充要条件是（　　）
    A．$sinα=\frac{1}{2}$B．$cosα=-\frac{{\sqrt{3}}}{2}$C．$tanα=-\frac{{\sqrt{3}}}{3}$D．$|PO|=\sqrt{3}+1$

    查看答案和解析>>

    同步练习册答案