
分析 设白球的个数为x,则红球和黑球的个数为10-x,记两个都不是白球的事件为A,
则至少有一个白球的事件与事件A为对立事件,由此求出白球的个数;
得出ξ的取值可能为0,1,2,3,求出ξ的分布列和数学期望.
解答 解:设白球的个数为x,则黑球和红球的个数为10-x;
记两个都不是白球的事件为A,则至少有一个白球的事件与事件A为对立事件;
所以p(A)=1-$\frac{7}{9}$=$\frac{2}{9}$=$\frac{{C}_{10-x}^{2}}{{C}_{10}^{2}}$,解得x=5,
所以白球的个数为5;
从袋中任意摸出3个球,到白球的个数ξ的取值可能为:0,1,2,3;
则P(ξ=0)=$\frac{{C}_{5}^{0}{•C}_{5}^{3}}{{C}_{10}^{3}}$=$\frac{1}{12}$,
P(ξ=1)=$\frac{{C}_{5}^{1}{•C}_{5}^{2}}{{C}_{10}^{3}}$=$\frac{5}{12}$,
P(ξ=2)=$\frac{{C}_{5}^{2}{•C}_{5}^{1}}{{C}_{10}^{3}}$=$\frac{5}{12}$,
P(ξ=3)=$\frac{{C}_{5}^{3}{•C}_{5}^{0}}{{C}_{10}^{3}}$=$\frac{1}{12}$,
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{5}{12}$ | $\frac{5}{12}$ | $\frac{1}{12}$ |
点评 本题考查了离散型随机变量的分布列与数学期望的计算问题,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 等腰三角形 | C. | 钝角三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数$y=sin(2x+\frac{π}{3})$在区间$(-\frac{π}{3},\frac{π}{6})$内单调递增 | |
| B. | 函数y=cos4x的最小正周期为2π | |
| C. | 函数y=cos(x+$\frac{π}{3}$)的图象是关于点($\frac{π}{6}$,0)成中心对称的图形 | |
| D. | 函数y=tan(x+$\frac{π}{3}$)的图象是关于直线x=$\frac{π}{6}$成轴对称的图形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
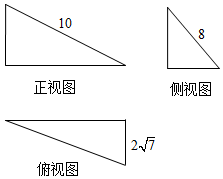
| A. | 32 | B. | $32\sqrt{7}$ | C. | $16\sqrt{7}$ | D. | $64\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{21}{4}$ | C. | $\frac{17}{4}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com