
【题目】平面内有12个点,其中任意三点不共线,每两点连一条线段(或边)。这些线段用红、蓝两色染色,每条线段恰染一色,其中,从某点![]() 出发的红色线段有奇数条,而从其余11个点出发的红色线段数互不相同。求以已知点为顶点、各边均为红色的三角形个数及两边为红色、另一边为蓝色的三角形个数。
出发的红色线段有奇数条,而从其余11个点出发的红色线段数互不相同。求以已知点为顶点、各边均为红色的三角形个数及两边为红色、另一边为蓝色的三角形个数。
【答案】40,55
【解析】
解法1 注意到从每点引出的红色线段只可能为0,1,…,11中的一种取值,而0、11不可能同时出现,从而,有两类可能情形:
(1)0,1,…,10;
(2)1,2,…,11.
若为情形(2),当点![]() 引出
引出![]() 条红色线段时,
条红色线段时,![]() 不是整数.从而,只可能为情形(1).
不是整数.从而,只可能为情形(1).
于是,除点![]() 外,另外11个点分别连出0,1,…,10条红色线段.
外,另外11个点分别连出0,1,…,10条红色线段.
此时,不妨设点![]() 连出
连出![]() 条红色线段(简称红边),
条红色线段(简称红边),![]() 连出
连出![]() 条红边.则点
条红边.则点![]() 与除了点
与除了点![]() 外的其余10个点
外的其余10个点![]() 均连了红边;点
均连了红边;点![]() 与除了点
与除了点![]() 外的其余9个点
外的其余9个点![]() 均连了红边.
均连了红边.
依此类推,点![]() 与除点
与除点![]() 外的8个点连了红边;点
外的8个点连了红边;点![]() 与除点
与除点![]() 外的7个点连了红边;点
外的7个点连了红边;点![]() 与除点
与除点![]() 外的6个点连了红边.从而,点
外的6个点连了红边.从而,点![]() 均为点
均为点![]() 连有红边.
连有红边.
由于点![]() 只连了5条红边(
只连了5条红边(![]() 与
与![]() 已连了红边),则点
已连了红边),则点![]() 不与点
不与点![]() 连红边.
连红边.
同理,点![]() 均不与点
均不与点![]() 连红边.
连红边.
故点![]() 处连了5条红边.
处连了5条红边.
令![]() ,
,![]() .
.
则![]() 中任意两点无红边相连,而
中任意两点无红边相连,而![]() 中任意两点均有红边相连,且
中任意两点均有红边相连,且![]() 中任一点
中任一点![]() 恰与
恰与![]() 中
中![]() 个点连有红边.因此,以
个点连有红边.因此,以![]() 为顶点且三边均为红边的三角形不存在,以
为顶点且三边均为红边的三角形不存在,以![]() 为顶点且三边均为红边的三角形有
为顶点且三边均为红边的三角形有![]() 个,以
个,以![]() 中任意三点为顶点且三边均为红边的三角形有
中任意三点为顶点且三边均为红边的三角形有![]() 个.故三边均为红边的三角形个数为
个.故三边均为红边的三角形个数为
![]() .
.
两边为红边、另一边为蓝边的三角形分为两类:
(ⅰ)三角形的一个顶点![]() ,另两个顶点属于
,另两个顶点属于![]() ,且从
,且从![]() 中一点
中一点![]() 向
向![]() 中两点引出的两边是一红、一蓝(
中两点引出的两边是一红、一蓝(![]() 中两点连线皆为红边).
中两点连线皆为红边).
这类三角形的个数为![]() .
.
(ⅱ)三角形的一个顶点为![]() (
(![]() 为
为![]() 或
或![]() ),另两个顶点属于
),另两个顶点属于![]() ,且从点
,且从点![]() 向
向![]() 中两点所引的均为红边(
中两点所引的均为红边(![]() 中两点连线均为蓝边).
中两点连线均为蓝边).
这类三角形的个数为![]() .
.
故两边为红色、另一边为蓝色的三角形有35+20=55个.
因此,所求个数分别为40、55.
解法2 同解法1知三边均为红色的三角形的个数为40.
对任何![]() ,以
,以![]() 为一个顶点且与
为一个顶点且与![]() 相连的两边均为红边的三角形的个数为
相连的两边均为红边的三角形的个数为![]() ,以
,以![]() 为一个顶点且与
为一个顶点且与![]() 相连的两边皆为红边的三角形的个数为
相连的两边皆为红边的三角形的个数为![]() ,将所有这些三角形的个数加起来得
,将所有这些三角形的个数加起来得![]() .
.
在以上的和中,每一个具有两条红边、一条蓝边的三角形只被计算一次,每个三边均为红边的三角形均被计算三次,
从而,两边为红色、一边为蓝色的三角形个数为175-3×40=55,故所求个数分别为40、55.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】下列叙述正确的是( )
A.相关关系是一种确定性关系,一般可分为正相关和负相关
B.回归直线一定过样本点的中心![]()
C.在回归分析中,![]() 为
为![]() 的模型比
的模型比![]() 为
为![]() 的模型拟合的效果好
的模型拟合的效果好
D.某同学研究卖出的热饮杯数![]() 与气温
与气温![]() (℃)时,一定可卖出
(℃)时,一定可卖出![]() 杯热饮
杯热饮
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列几个命题,是真命题有( )
A.若![]() ,则
,则![]()
B.若复数![]() ,
,![]() 满足
满足![]() ,则
,则![]()
C.给定两个命题![]() ,
,![]() .若
.若![]() 是
是![]() 的必要而不充分条件,则
的必要而不充分条件,则![]() 是
是![]() 的充分不必要条件
的充分不必要条件
D.命题![]() :
:![]() ,
,![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() +y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
+y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
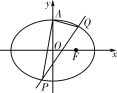
(1)求椭圆C的方程;
(2)若不过点A的动直线l与椭圆C相交于P,Q两点,且![]() =0,求证:直线l过定点,并求出该定点N的坐标.
=0,求证:直线l过定点,并求出该定点N的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱![]() 的底面是边长为2的正三角形,侧棱
的底面是边长为2的正三角形,侧棱![]() 与下底面相邻的两边AB,AC均成45度的角.
与下底面相邻的两边AB,AC均成45度的角.
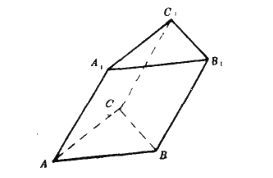
(1)求点![]() 到平面B1BCC1的距离.
到平面B1BCC1的距离.
(2)试问,当![]() 为多长时,点
为多长时,点![]() 到平面
到平面![]() 与到平面
与到平面![]() 的距离相等.
的距离相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】21世纪城的街道都是东西向和南北向,为了加强安全管理,在一些十字路口设置保安亭(任何两个保安亭都不在同一街道上),以两个保安亭为其两个顶点、街道为边围成的矩形称为一个安全区,安全区(包括边界)内保安亭的个数称为该安全区的安全强度.如果世纪城两个方向的街道都至少有![]() 条,且任何两条不平行的街道都交成一个十字路口,今按要求选定
条,且任何两条不平行的街道都交成一个十字路口,今按要求选定![]() 个十字路口设置保安亭,求安全强度最大的安全区的安全强度的最小值.
个十字路口设置保安亭,求安全强度最大的安全区的安全强度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com