
已知函数f(x)=ln x-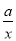 .
.
(1)当a>0时,判断f(x)在定义域上的单调性;
(2)f(x)在[1,e]上的最小值为 ,求实数a的值;
,求实数a的值;
(3)试求实数a的取值范围,使得在区间(1,+∞)上函数y=x2的图象恒在函数y=f(x)图象的上方.
(1)f(x)在(0,+∞)上是单调递增函数
(2)a=- (3)a≥-1
(3)a≥-1
【解析】(1)f′(x)=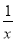 +
+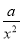 =
= (x>0),
(x>0),
当a>0时,f′(x)>0恒成立,
故f(x)在(0,+∞)上是单调递增函数.
(2)由f′(x)=0得x=-a,
①当a≥-1时,f′(x)≥0在[1,e]上恒成立,f(x)在[1,e]上为增函数.
f(x)min=f(1)=-a=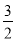 得a=-
得a=-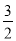 (舍).
(舍).
②当a≤-e时,f′(x)≤0在[1,e]上恒成立,f(x)在[1,e]上为减函数.
则f(x)min=f(e)=1-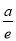 =
=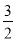 得a=-
得a=-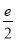 (舍).
(舍).
③当-e<a<-1时,由f′(x)=0得x0=-a.
当1<x<x0时,f′(x)<0,f(x)在(1,x0)上为减函数;
当x0<x<e时,f′(x)>0,f(x)在(x0,e)上为增函数.
∴f(x)min=f(-a)=ln(-a)+1=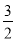 ,得a=-
,得a=-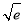 .
.
综上知:a=- .
.
(3)由题意得:x2>ln x-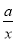 在(1,+∞)上恒成立,
在(1,+∞)上恒成立,
即a>xln x-x3在(1,+∞)上恒成立.
设g(x)=xln x-x3(x>1),则
g′(x)=ln x-3x2+1.
令h(x)=ln x-3x2+1,则
h′(x)=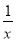 -6x.
-6x.
当x>1时,h′(x)<0恒成立.
∴h(x)=g′(x)=ln x-3x2+1在(1,+∞)上为减函数,
则g′(x)<g′(1)=-2<0.
所以g(x)在(1,+∞)上为减函数,
∴g(x)<g(1)<-1,故a≥-1


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(四)(解析版) 题型:选择题
已知α,β表示两个不同的平面,m是一条直线且m?α,则:“α⊥β”是“m⊥β”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(五)(解析版) 题型:选择题
已知a≤ +ln x对任意x∈[
+ln x对任意x∈[ ,2]恒成立,则a的最大值为( )
,2]恒成立,则a的最大值为( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(二)(解析版) 题型:选择题
给出下列四个命题,其中不正确的命题为( )
①若cos α=cos β,则α-β=2kπ,k∈Z;
②函数y=2cos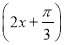 的图象关于x=
的图象关于x=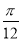 对称;
对称;
③函数y=cos(sin x)(x∈R)为偶函数;
④函数y=sin|x|是周期函数,且周期为2π.
A.①② B.①④ C.①②③ D.①②④
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(二)(解析版) 题型:选择题
若函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[-1,1]时,f(x)=|x|,函数g(x)= ,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
A.10 B.9 C.8 D.7
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(三)(解析版) 题型:解答题
设函数f(x)=cos +2cos2
+2cos2 ,x∈R.
,x∈R.
(1)求f(x)的值域;
(2)记△ABC的内角A、B、C的对边长分别为a、b、c,若f(B)=1,b=1,c= ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(三)(解析版) 题型:选择题
已知g(x)=loga|x+1|(a>0且a≠1)在(-1,0)上有g(x)>0,则f(x)=a|x-1|( )
A.在(-∞,0)上是递增的
B.在(-∞,0)上是递减的
C.在(-∞,-1)上是递增的
D.在(-∞,-1)上是递减的
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(一)(解析版) 题型:填空题
函数y=f(x)为定义在R上的减函数,函数y=f(x-1)的图象关于点(1,0)对称,x,y满足不等式f(x2-2x)+f(2y-y2)≤0,M(1,2),N(x,y),O为坐标原点,则当1≤x≤4时, 的取值范围为________.
的取值范围为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第十章 算法初步、统计、统计案例(解析版) 题型:解答题
做抛掷两颗骰子的试验:用(x,y)表示结果,其中x表示第一颗骰子出现的点数,y表示第二颗骰子出现的点数,(1)写出试验的基本事件;(2)求事件“出现点数之和大于8”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com