
【题目】已知函数f(x)=(λx+1)ln x-x+1.
(1)若λ=0,求f(x)的最大值;
(2)若曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直,证明:![]() >0.
>0.
【答案】见解析
【解析】(1)f(x)的定义域为(0,+∞),
当λ=0时,f(x)=ln x-x+1.
则f′(x)=![]() -1,令f′(x)=0,解得x=1.
-1,令f′(x)=0,解得x=1.
当0<x<1时,f′(x)>0,∴f(x)在(0,1)上是增函数;
当x>1时,f′(x)<0,∴f(x)在(1,+∞)上是减函数.
故f(x)在x=1处取得最大值f(1)=0.
(2)证明:由题可得,f′(x)=λln x+![]() -1.
-1.
由题设条件,得f′(1)=1,即λ=1.
∴f(x)=(x+1)ln x-x+1.
由(1)知,ln x-x+1<0(x>0,且x≠1).
当0<x<1时,f(x)=(x+1)ln x-x+1=xln x+(ln x-x+1)<0,
![]() >0.
>0.
当x>1时,f(x)=ln x+(xln x-x+1)=ln x-x![]() >0,∴
>0,∴![]() >0.
>0.
综上可知,![]() >0.
>0.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)设![]() ,当
,当![]() 时,求函数
时,求函数![]() 的定义域,判断并证明函数
的定义域,判断并证明函数![]() 的奇偶性;
的奇偶性;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 递减,并且最小值为1,若存在,求出
递减,并且最小值为1,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln x-ax(a∈R)(e=2.718 28…是自然对数的底数).
(1)判断f(x)的单调性;
(2)当f(x)<0在(0,+∞)上恒成立时,求a的取值范围;
(3)证明:当x∈(0,+∞)时,![]() (1+x)
(1+x) ![]() <e.
<e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并得到如下频率分布直方图.
,并得到如下频率分布直方图.
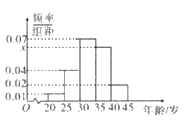
(I)求图中![]() 的值,并根据频率分布直方图统计这600名志愿者中年龄在
的值,并根据频率分布直方图统计这600名志愿者中年龄在![]() 的人数;
的人数;
(II)在抽取的100名志愿者中按年龄分层抽取5名参加区电视台“文明伴你行”节目录制,再从这5名志愿者中随机抽取2名到现场分享劝导制止行人闯红灯的经历,求至少有1名年龄不低于35岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(2)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三上学期期末数学考试成绩中,随机抽取了![]() 名学生的成绩得到如图所示的频率分布直方图:
名学生的成绩得到如图所示的频率分布直方图:
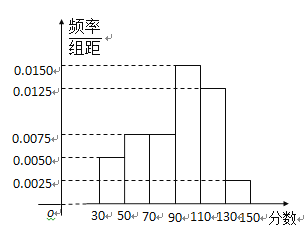
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在![]() 和
和![]() 的学生中共抽取
的学生中共抽取![]() 人,该
人,该![]() 人中成绩在
人中成绩在![]() 的有几人?
的有几人?
(3)在(2)中抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求分数在
人,求分数在![]() 和
和![]() 各
各![]() 人的概率.
人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com