
| A.11元 | B.12元 | C.13元 | D.14元 |
科目:高中数学 来源:不详 题型:解答题
 ,其中a为大于零的常数.
,其中a为大于零的常数. +
+ +…+
+…+ 恒成立.
恒成立. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和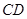 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 所在圆的半径为10米.设小圆弧
所在圆的半径为10米.设小圆弧 所在圆的半径为
所在圆的半径为 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
 关于
关于 的函数关系式;
的函数关系式; ,当
,当 为何值时,
为何值时, 取得最大值?
取得最大值?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的隧道时,整个车身都在隧道里的时间是
的隧道时,整个车身都在隧道里的时间是 .该列车以同样的速度穿过长790
.该列车以同样的速度穿过长790 的铁桥时,从车头上桥,到车尾下桥,共用时
的铁桥时,从车头上桥,到车尾下桥,共用时 ,则这列火车的长度为___
,则这列火车的长度为___ .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使 对 一切实数x均成 立,则称
对 一切实数x均成 立,则称 为“倍约束函数”,现给出下列函数:①
为“倍约束函数”,现给出下列函数:① :②
:②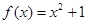 :③
:③ ;④
;④ ⑤
⑤ 是定义在实数集R上的奇函数,且
是定义在实数集R上的奇函数,且 均有
均有 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( )| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.y=x2 | B.y=x+1 | C.y=2x | D.y=log2|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com