
 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使 对 一切实数x均成 立,则称
对 一切实数x均成 立,则称 为“倍约束函数”,现给出下列函数:①
为“倍约束函数”,现给出下列函数:① :②
:②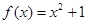 :③
:③ ;④
;④ ⑤
⑤ 是定义在实数集R上的奇函数,且
是定义在实数集R上的奇函数,且 均有
均有 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( )| A.1个 | B.2个 | C.3个 | D.4个 |
科目:高中数学 来源:不详 题型:单选题
 ,使得对定义域
,使得对定义域 内的任意两个
内的任意两个 ,均有
,均有 成立,则称函数
成立,则称函数 在定义域
在定义域 上满足利普希茨条件.若函数
上满足利普希茨条件.若函数 满足利普希茨条件,则常数
满足利普希茨条件,则常数 的最小值为()
的最小值为()| A.4 | B.3 | C.1 | D.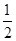 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 在区间
在区间 上的导函数为
上的导函数为 ,
, 在区间
在区间 上的导函数为
上的导函数为 ,若在区间
,若在区间 上
上 恒成立,则称函数
恒成立,则称函数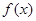 在区间
在区间 上为“凸函数”.已知
上为“凸函数”.已知 ,若对任意的实数
,若对任意的实数 满足
满足 时,函数
时,函数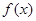 在区间上
在区间上 为“凸函数”,则
为“凸函数”,则 的最大值为( )
的最大值为( )| A.4 | B.3 | C.2 | D.1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
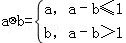 .设函数f(x)=(x2﹣2)?(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
.设函数f(x)=(x2﹣2)?(x﹣x2),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )A. |
B. |
C. |
D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.11元 | B.12元 | C.13元 | D.14元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
, ,沿对角线AC折成如图所示的四面体,二面角B-AC-D为
,沿对角线AC折成如图所示的四面体,二面角B-AC-D为 ,M为AC的中点,P在线段DM上,记DP=x,PA+PB=y,则函数y=f(x)的图象大致为( )
,M为AC的中点,P在线段DM上,记DP=x,PA+PB=y,则函数y=f(x)的图象大致为( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com