
ЎѕМвДїЎїИзНјЈ¬ДіКРЧј±ёФЪµАВ·![]() µДТ»ІаРЮЅЁТ»МхФЛ¶Ї±ИИьµАЈ¬ИьµАµДЗ°Т»Ії·ЦОЄЗъПЯ¶О
µДТ»ІаРЮЅЁТ»МхФЛ¶Ї±ИИьµАЈ¬ИьµАµДЗ°Т»Ії·ЦОЄЗъПЯ¶О![]() Ј¬ёГЗъПЯ¶ОКЗєЇКэ
Ј¬ёГЗъПЯ¶ОКЗєЇКэ![]() Ј¬
Ј¬ ![]() К±µДНјПуЈ¬ЗТНјПуµДЧоёЯµгОЄ
К±µДНјПуЈ¬ЗТНјПуµДЧоёЯµгОЄ![]() .ИьµАµДЦРјдІї·ЦОЄі¤
.ИьµАµДЦРјдІї·ЦОЄі¤![]() З§ГЧµДЦ±ПЯЕЬµА
З§ГЧµДЦ±ПЯЕЬµА![]() Ј¬ЗТ
Ј¬ЗТ![]() .ИьµАµДєуТ»Ії·ЦКЗТФ
.ИьµАµДєуТ»Ії·ЦКЗТФ![]() ОЄФІРДµДТ»¶ОФІ»Ў
ОЄФІРДµДТ»¶ОФІ»Ў![]() .
.
(1)Зу![]() µДЦµєН
µДЦµєН![]() µДґуРЎЈ»
µДґуРЎЈ»
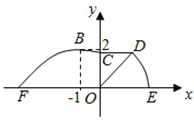
(2)ИфТЄФЪФІ»ЎИьµАЛщ¶ФУ¦µДЙИРО![]() ЗшУтДЪЅЁТ»ёцЎ°ѕШРОІЭЖєЎ±Ј¬ѕШРОµДТ»±ЯФЪµАВ·
ЗшУтДЪЅЁТ»ёцЎ°ѕШРОІЭЖєЎ±Ј¬ѕШРОµДТ»±ЯФЪµАВ·![]() ЙПЈ¬Т»ёц¶ҐµгФЪ°лѕ¶
ЙПЈ¬Т»ёц¶ҐµгФЪ°лѕ¶![]() ЙПЈ¬БнНвТ»ёц¶Ґµг
ЙПЈ¬БнНвТ»ёц¶Ґµг![]() ФЪФІ»Ў
ФЪФІ»Ў![]() ЙПЈ¬ЗТ
ЙПЈ¬ЗТ![]() ,Зуµ±Ў°ѕШРОІЭЖєЎ±µДГж»эИЎЧоґуЦµК±
,Зуµ±Ў°ѕШРОІЭЖєЎ±µДГж»эИЎЧоґуЦµК±![]() µДЦµ.
µДЦµ.
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј¬
Ј¬ ![]() Ј»ЈЁ2Ј©
Ј»ЈЁ2Ј©![]() .
.
ЎѕЅвОцЎїКФМв·ЦОцЈє
ЈЁ1Ј©УЙМвТвїЙµГ![]() Ј¬№К
Ј¬№К![]() Ј¬ґУ¶шїЙµГЗъПЯ¶О
Ј¬ґУ¶шїЙµГЗъПЯ¶О![]() µДЅвОцКЅОЄ
µДЅвОцКЅОЄ![]() Ј¬Боx=0їЙµГ
Ј¬Боx=0їЙµГ![]() Ј¬ёщѕЭ
Ј¬ёщѕЭ![]() Ј¬µГ
Ј¬µГ![]() ,ТтґЛ
,ТтґЛ![]() ЈЁ2Ј©ЅбєПМвТвїЙµГµ±Ў°ѕШРОІЭЖєЎ±µДГж»эЧоґуК±Ј¬µг
ЈЁ2Ј©ЅбєПМвТвїЙµГµ±Ў°ѕШРОІЭЖєЎ±µДГж»эЧоґуК±Ј¬µг![]() ФЪ»Ў
ФЪ»Ў![]() ЙПЈ¬УЙМхјюїЙµГЎ°ѕШРОІЭЖєЎ±µДГж»эОЄ
ЙПЈ¬УЙМхјюїЙµГЎ°ѕШРОІЭЖєЎ±µДГж»эОЄ![]() Ј¬И»єуёщѕЭ
Ј¬И»єуёщѕЭ![]() µД·¶О§їЙµГµ±
µД·¶О§їЙµГµ±![]() К±Ј¬
К±Ј¬![]() ИЎµГЧоґуЦµЈ®
ИЎµГЧоґуЦµЈ®
КФМвЅвОцЈє
(1)УЙМхјюµГ![]() .
.
Ўа![]() .
.
ЎаЗъПЯ¶О![]() µДЅвОцКЅОЄ
µДЅвОцКЅОЄ![]() .
.
µ±![]() К±Ј¬
К±Ј¬![]() .
.
УЦ![]() Ј¬
Ј¬
Ўа![]() ,
,
Ўа![]() .
.
(2)УЙ(1)Ј¬їЙЦЄ![]() .
.
УЦТЧЦЄµ±Ў°ѕШРОІЭЖєЎ±µДГж»эЧоґуК±Ј¬µг![]() ФЪ»Ў
ФЪ»Ў![]() ЙПЈ¬№К
ЙПЈ¬№К![]() .
.
Йи![]() ,
,![]() ,Ў°ѕШРОІЭЖєЎ±µДГж»эОЄ
,Ў°ѕШРОІЭЖєЎ±µДГж»эОЄ
![]()
![]() .
.
ЎЯ![]() Ј¬
Ј¬
Ўа![]() ,
,
№Кµ±![]() Ј¬јґ
Ј¬јґ![]() К±Ј¬
К±Ј¬![]() ИЎµГЧоґуЦµЈ®
ИЎµГЧоґуЦµЈ®


 їЪЛгМвїЁ±±ѕ©ёѕЕ®¶щНЇіц°жЙзПµБРґр°ё
їЪЛгМвїЁ±±ѕ©ёѕЕ®¶щНЇіц°жЙзПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіµзЧУЙМОс№«Лѕ¶Ф10 000ГыНшВз№єОпХЯ2017Дк¶ИµДПы·СЗйїцЅшРРНіјЖ,·ўПЦПы·СЅр¶о(µҐО»:НтФЄ)¶јФЪЗшјд[0.3,0.9]ДЪ,ЖдЖµВК·ЦІјЦ±·ЅНјИзНјЛщКѕ.
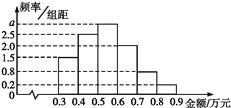
(1)Ц±·ЅНјЦРµДa=_____;
(2)ФЪХвР©№єОпХЯЦР,Пы·СЅр¶оФЪЗшјд[0.5,0.9]ДЪµД№єОпХЯµДИЛКэОЄ_______.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї¶ЁТеЎ°ИэЅЗБµРґ·ЁЎ±ОЄЎ°ИэёцИЛЦ®јдРґРЕЈ¬ГїИЛёшБнНвБЅИЛЦ®Т»РґТ»·вРЕЈ¬ЗТИОТвБЅёцИЛІ»»б±ЛґЛёш¶Ф·ЅРґРЕЎ±Ј¬ИфОеёцИЛaЈ¬bЈ¬cЈ¬dЈ¬eЦРµДГїёцИЛ¶јЗЎёшЖдУаЛДИЛЦРµДДіТ»ёцИЛРґБЛТ»·вРЕЈ¬ФтІ»іцПЦЎ°ИэЅЗБµРґ·ЁЎ±Рґ·ЁµДРґРЕЗйїцµДЦЦКэОЄЈЁ Ј©
A.704
B.864
C.1004
D.1014
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪИэАвЦщABC©ЃA1B1C1ЦРЈ¬µЧГжЎчABCКЗµИ±ЯИэЅЗРОЈ¬ІаГжAA1B1BОЄХэ·ЅРОЈ¬ЗТAA1ЎНЖЅГжABCЈ¬DОЄПЯ¶ОABЙПµДТ»µгЈ® 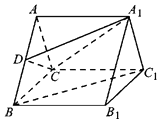
ЈЁўсЈ©ИфBC1ЎОЖЅГжA1CDЈ¬И·¶ЁDµДО»ЦГЈ¬ІўЛµГчАнУЙЈ»
ЈЁўтЈ©ФЪЈЁўсЈ©µДМхјюПВЈ¬Зу¶юГжЅЗA1D©ЃC©ЃBC1µДУаПТЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэfЈЁxЈ©=|x©Ѓ5|©Ѓ|x©Ѓ2|Ј®
ЈЁ1Ј©ИфxЎКRЈ¬К№µГfЈЁxЈ©ЎЬmіЙБўЈ¬ЗуmµД·¶О§Ј»
ЈЁ2Ј©ЗуІ»µИКЅx2©Ѓ8x+15+fЈЁxЈ©ЎЬ0µДЅвјЇЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() ЈЁ
ЈЁ![]() Ј©КЗЕјєЇКэЈ®
Ј©КЗЕјєЇКэЈ®
ЈЁ1Ј©Зу![]() µДЦµЈ»
µДЦµЈ»
ЈЁ2Ј©ИфєЇКэ![]() Г»УРБгµгЈ¬Зу
Г»УРБгµгЈ¬Зу![]() µДИЎЦµ·¶О§Ј»
µДИЎЦµ·¶О§Ј»
ЈЁ3Ј©ИфєЇКэ![]() Ј¬
Ј¬ ![]() µДЧоРЎЦµОЄ0Ј¬ЗуКµКэ
µДЧоРЎЦµОЄ0Ј¬ЗуКµКэ![]() µДЦµЈ®
µДЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄxЎК[©Ѓ1Ј¬0]Ј¬¦ИЎК[0Ј¬2¦РЈ©Ј¬¶юФЄєЇКэ ![]() ИЎЧоРЎЦµК±Ј¬x=x0 Ј¬ ¦И=¦И0ФтЈЁ Ј©
ИЎЧоРЎЦµК±Ј¬x=x0 Ј¬ ¦И=¦И0ФтЈЁ Ј©
A.4x0+¦И0=0
B.4x0+¦И0Јј0
C.4x0+¦И0Јѕ0
D.ТФЙПѕщУРїЙДЬЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНј1Ј¬ФЪ![]() ЦР,
ЦР, ![]() ·Ц±рОЄ
·Ц±рОЄ![]() µДЦРµгЈ¬µг
µДЦРµгЈ¬µг![]() ОЄПЯ¶О
ОЄПЯ¶О![]() ЙПµДТ»µгЈ¬Ѕ«
ЙПµДТ»µгЈ¬Ѕ«![]() СШ
СШ![]() ХЫЖрµЅ
ХЫЖрµЅ![]() µДО»ЦГЈ¬К№
µДО»ЦГЈ¬К№![]() Ј¬ИзНј2.
Ј¬ИзНј2.
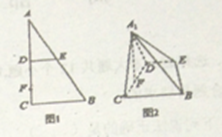
ЈЁ1Ј©ЗуЦ¤Јє ![]() Ј»
Ј»
ЈЁ2Ј©ПЯ¶О![]() ЙПКЗ·сґжФЪµг
ЙПКЗ·сґжФЪµг![]() Ј¬К№
Ј¬К№![]() ЖЅГж
ЖЅГж![]() ЈїЛµГчАнУЙ.
ЈїЛµГчАнУЙ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЙиU=RЈ¬A={x|xЎЬ2Ј¬»тxЎЭ5}Ј¬B= ![]() Ј¬C={x|aЈјxЈјa+1}
Ј¬C={x|aЈјxЈјa+1}
ЈЁ1Ј©ЗуAЎИBєНЈЁUAЈ©ЎЙB
ЈЁ2Ј©ИфBЎЙC=CЈ¬ЗуКµКэaµДИЎЦµ·¶О§Ј®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com