
【题目】已知抛物线![]() =
=![]() 的焦点
的焦点![]() 为坐标原点,
为坐标原点, ![]() 是抛物线
是抛物线![]() 上异于
上异于![]() 的两点.
的两点.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 的斜率之积为
的斜率之积为![]() ,求证:直线
,求证:直线![]() 过
过![]() 轴上一定点.
轴上一定点.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:本题主要考查抛物线方程、直线与圆锥曲线的位置关系、直线的方程与斜率,考查了定点问题.(1)由抛物线的焦点坐标可得p的值,即可得抛物线方程;(2)分直线的斜率存在与不存在两种情况,结合直线![]() 的斜率之积为
的斜率之积为![]() 进行讨论.
进行讨论.
试题解析:
(1)因为抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以抛物线![]() 的方程为
的方程为![]() .
.
(2)证明:①当直线![]() 的斜率不存在时,
的斜率不存在时,
设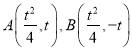 .
.
因为直线![]() 的斜率之积为
的斜率之积为![]() ,
,
所以![]() =
=![]() ,化简得
,化简得![]() ,
,
所以![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.
②当直线![]() 的斜率存在时,
的斜率存在时,
设其方程为![]() =
= ![]() ,
,
联立方程组![]() 消去
消去![]() ,
,
得![]() ,
,
根据根与系数的关系得![]() ,因为直线
,因为直线![]() 的斜率之积为
的斜率之积为![]() ,
,
所以![]() =
=![]() ,即
,即![]() ,即
,即![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
所以![]() =
=![]() =
=![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ,
,
综上所述,直线![]() 过定点
过定点![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆方程;
(2)设不过原点![]() 的直线
的直线![]() ,与该椭圆交于
,与该椭圆交于![]() 两点,直线
两点,直线![]() 的斜率依次为
的斜率依次为![]() ,满足
,满足![]() ,试问:当
,试问:当![]() 变化时,
变化时,![]() 是否为定值?若是,求出此定值,并证明你的结论;若不是请说明理由.
是否为定值?若是,求出此定值,并证明你的结论;若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin![]() (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求函数f(x)的单调增区间;
(2)将函数f(x)的图象向左平移![]() 个单位长度,再向上平移1个单位长度,得到函数y=g(x)的图象.求y=g(x)在区间[0,10π]上零点的个数.
个单位长度,再向上平移1个单位长度,得到函数y=g(x)的图象.求y=g(x)在区间[0,10π]上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() 1(a>
1(a> ![]() )的右焦点为F,右顶点为A,已知
)的右焦点为F,右顶点为A,已知 ![]() ,其中O为原点,e为椭圆的离心率.
,其中O为原点,e为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点A的直线l与椭圆交于B(B不在x轴上),垂直于l的直线与l交于点M,与y轴交于点H,若BF⊥HF,且∠MOA=∠MAO,求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面![]() 与平面
与平面![]() 交于直线
交于直线![]() 是平面
是平面![]() 内不同的两点,
内不同的两点,![]() 是平面
是平面![]() 内不同的两点,且
内不同的两点,且![]() 不在直线
不在直线![]() 上,
上,![]() 分别是线段
分别是线段![]() 的中点,下列命题中正确的个数为( )
的中点,下列命题中正确的个数为( )
①若![]() 与
与![]() 相交,且直线
相交,且直线![]() 平行于
平行于![]() 时,则直线
时,则直线![]() 与
与![]() 也平行;
也平行;
②若![]() 是异面直线时,则直线
是异面直线时,则直线![]() 可能与
可能与![]() 平行;
平行;
③若![]() 是异面直线时,则不存在异于
是异面直线时,则不存在异于![]() 的直线同时与直线
的直线同时与直线![]() 都相交;
都相交;
④![]() 两点可能重合,但此时直线
两点可能重合,但此时直线![]() 与
与![]() 不可能相交
不可能相交

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,点M(m, 0)在x轴的正半轴上,过M点的直线
,点M(m, 0)在x轴的正半轴上,过M点的直线![]() 与抛物线 C相交于A,B两点,O为坐标原点.
与抛物线 C相交于A,B两点,O为坐标原点.
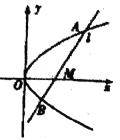
(1) 若m=l,且直线![]() 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(2) 是否存在定点M,使得不论直线![]() 绕点M如何转动,
绕点M如何转动, ![]() 恒为定值?
恒为定值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:x2+y2-4x-2y-5=0与圆C2:x2+y2-6x-y-9=0.
(1)求证:两圆相交;(2)求两圆公共弦所在的直线方程;
(3)在平面上找一点P,过P点引两圆的切线并使它们的长都等于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABNCD,EF∥AB,AB=2,BC=EF=1,AE= ![]() ,∠BAD=60°,G为BC的中点.
,∠BAD=60°,G为BC的中点. 
(1)求证:FG∥平面BED;
(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com