
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABNCD,EF∥AB,AB=2,BC=EF=1,AE= ![]() ,∠BAD=60°,G为BC的中点.
,∠BAD=60°,G为BC的中点. 
(1)求证:FG∥平面BED;
(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
【答案】
(1)
证明:BD的中点为O,

连接OE,OG,在△BCD中,
∵G是BC的中点,
∴OG∥DC,且OG= ![]() DC=1,
DC=1,
又∵EF∥AB,AB∥DC,
∴EF∥OG,且EF=0G,
即四边形OGEF是平行四边形,
∴FG∥OE,
∵FG平面BED,OE平面BED,
∴FG∥平面BED;
(2)
证明:在△ABD中,AD=1,AB=2,∠BAD=60°,
由余弦定理可得BD= ![]() ,仅而∠ADB=90°,
,仅而∠ADB=90°,
即BD⊥AD,
又∵平面AED⊥平面ABCD,
BD平面ABCD,平面AED∩平面ABCD=AD,
∴BD⊥平面AED,
∵BD平面BED,
∴平面BED⊥平面AED
(3)
解:∵EF∥AB,
∴直线EF与平面BED所成的角即为直线AB与平面BED所形成的角,
过点A作AH⊥DH于点H,连接BH,
又平面BED∩平面AED=ED,
由(2)知AH⊥平面BED,
∴直线AB与平面BED所成的为∠ABH,
在△ADE,AD=1,DE=3,AE= ![]() ,由余弦定理得cos∠ADE=
,由余弦定理得cos∠ADE= ![]() ,
,
∴sin∠ADE= ![]() ,
,
∴AH=AD ![]() ,
,
在Rt△AHB中,sin∠ABH= ![]() =
= ![]() ,
,
∴直线EF与平面BED所成角的正弦值 ![]()
【解析】(1)利用中位线定理,和平行公理得到四边形OGEF是平行四边形,再根据线面平行的判定定理即可证明;
(2)根据余弦定理求出BD= ![]() ,继而得到BD⊥AD,再根据面面垂直的判定定理即可证明;
,继而得到BD⊥AD,再根据面面垂直的判定定理即可证明;
(3)先判断出直线EF与平面BED所成的角即为直线AB与平面BED所形成的角,再根据余弦定理和解直角三角形即可求出答案.
本题考查了直线与平面的平行和垂直,平面与平面的垂直,直线与平面所成的角,考查了空间想象能力,运算能力和推理论证能力,属于中档题.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(![]() sinx-cosx)+m(m∈R),将y=f(x)的图象向左平移
sinx-cosx)+m(m∈R),将y=f(x)的图象向左平移![]() 个单位后得到g(x)的图象,且y=g(x)在区间[
个单位后得到g(x)的图象,且y=g(x)在区间[![]() ]内的最小值为
]内的最小值为![]() .
.
(1)求m的值;
(2)在锐角△ABC中,若g(![]() )=
)=![]() ,求sinA+cosB的取值范围.
,求sinA+cosB的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】铜仁市某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100]分别加以统计,得到如图所示的频率分布直方图.

(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
K2=
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l:x-y-2=0,抛物线C:y2=2px(p>0).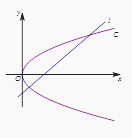
(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证:线段PQ的中点坐标为(2-p , -p);
②求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() )的图象与
)的图象与![]() 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为![]() ,且图象上一个最低点为
,且图象上一个最低点为![]() .
.
(1)求![]() 的解析式,对称轴及对称中心.
的解析式,对称轴及对称中心.
(2)该图象可以由![]() 的图象经过怎样的变化得到.
的图象经过怎样的变化得到.
(3)当![]() ,求
,求![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:x2+y2﹣2ay=0(a>0)截直线x+y=0所得线段的长度是2 ![]() ,则圆M与圆N:(x﹣1)2+(y﹣1)2=1的位置关系是( )
,则圆M与圆N:(x﹣1)2+(y﹣1)2=1的位置关系是( )
A.内切
B.相交
C.外切
D.相离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .直角梯形
.直角梯形![]() 通过直角梯形
通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且使平面
为轴旋转得到,且使平面![]() 平面
平面![]() .
. ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点.
上的动点.

(1)求证: ![]() ;
;
(2)当点![]() 是线段
是线段![]() 中点时,求二面角
中点时,求二面角![]() 的余弦值;
的余弦值;
(3)是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,M是矩形ABCD的边CD上的一点,AC与BM交于点N,BN=![]() BM.
BM.

(1)求证:M是CD的中点;
(2)若AB=2,BC=1,H是BM上异于点B的一动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com