
【题目】已知函数f(x)=cosx(![]() sinx-cosx)+m(m∈R),将y=f(x)的图象向左平移
sinx-cosx)+m(m∈R),将y=f(x)的图象向左平移![]() 个单位后得到g(x)的图象,且y=g(x)在区间[
个单位后得到g(x)的图象,且y=g(x)在区间[![]() ]内的最小值为
]内的最小值为![]() .
.
(1)求m的值;
(2)在锐角△ABC中,若g(![]() )=
)=![]() ,求sinA+cosB的取值范围.
,求sinA+cosB的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据二倍角公式化简![]() ,利用平移规律得出
,利用平移规律得出![]() 的解析式,根据最小值列方程求出
的解析式,根据最小值列方程求出![]() ;
;
(2)根据条件求出![]() ,用
,用![]() 表示出
表示出![]() ,化简
,化简![]() 得出关于
得出关于![]() 函数,根据
函数,根据![]() 的范围得出正弦函数的性质得出
的范围得出正弦函数的性质得出![]() 的范围.
的范围.
(1)f(x)=![]() sinxcosx-cos2x+m=
sinxcosx-cos2x+m=![]() sin2x-cos2x+m-=sin(2x-)+m-,
sin2x-cos2x+m-=sin(2x-)+m-,
∴g(x)=sin[2(x+)-]+m-=sin(2x+)+m-,
∵x∈[,],∴2x+∈[![]() ,
,![]() ],
],
∴当2x+=![]() 时,g(x)取得最小值+m-=m,
时,g(x)取得最小值+m-=m,
∴m=![]() .
.
(2)∵g()=sin(C+)+![]() -=-+
-=-+![]() ,
,
∴sin(C+)=![]() ,
,
∵C∈(0,),∴C+∈(,![]() ),
),
∴C+=,即C=.
∴sinA+cosB=sinA+cos(![]() -A)
-A)
=sinA-![]() cosA+sinA
cosA+sinA
=sinA-![]() cosA
cosA
=![]() sin(A-).
sin(A-).
∵△ABC是锐角三角形,∴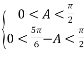 ,
,
解得![]() ,
,
∴A-∈(,),
∴<sin(A-)<![]() ,
,
∴![]() <
<![]() sin(A-)<,
sin(A-)<,
∴sinA+cosB的取值范围是(![]() ,).
,).


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin![]() (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求函数f(x)的单调增区间;
(2)将函数f(x)的图象向左平移![]() 个单位长度,再向上平移1个单位长度,得到函数y=g(x)的图象.求y=g(x)在区间[0,10π]上零点的个数.
个单位长度,再向上平移1个单位长度,得到函数y=g(x)的图象.求y=g(x)在区间[0,10π]上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,点M(m, 0)在x轴的正半轴上,过M点的直线
,点M(m, 0)在x轴的正半轴上,过M点的直线![]() 与抛物线 C相交于A,B两点,O为坐标原点.
与抛物线 C相交于A,B两点,O为坐标原点.
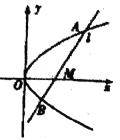
(1) 若m=l,且直线![]() 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(2) 是否存在定点M,使得不论直线![]() 绕点M如何转动,
绕点M如何转动, ![]() 恒为定值?
恒为定值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:x2+y2-4x-2y-5=0与圆C2:x2+y2-6x-y-9=0.
(1)求证:两圆相交;(2)求两圆公共弦所在的直线方程;
(3)在平面上找一点P,过P点引两圆的切线并使它们的长都等于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左顶点为
,左顶点为![]() ,过原点且斜率不为0的直线与椭圆交于
,过原点且斜率不为0的直线与椭圆交于![]() 两点,其中点
两点,其中点![]() 在第二象限,过点
在第二象限,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() .
.

⑴求椭圆的标准方程;
⑵当直线![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 的面积;
的面积;
⑶试比较![]() 与
与![]() 大小.
大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B,P在单位圆上,且![]()
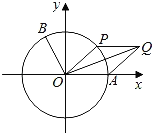
(1)求![]() 的值;
的值;
(2)设![]()
![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,
,![]() ,求
,求![]() 的最值及此时
的最值及此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABNCD,EF∥AB,AB=2,BC=EF=1,AE= ![]() ,∠BAD=60°,G为BC的中点.
,∠BAD=60°,G为BC的中点. 
(1)求证:FG∥平面BED;
(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx,则“b<0”是“f(f(x))的最小值与f(x)的最小值相等”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com