
【题目】如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B,P在单位圆上,且![]()
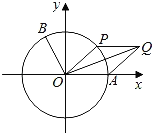
(1)求![]() 的值;
的值;
(2)设![]()
![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,
,![]() ,求
,求![]() 的最值及此时
的最值及此时![]() 的值.
的值.
【答案】(1)-10;(2)当![]() 时,
时,![]() ,当
,当![]() 时
时![]()
【解析】
![]() 由三角函数的定义可得
由三角函数的定义可得![]() 的值,将原式化为关于
的值,将原式化为关于![]() 的函数并代入
的函数并代入![]() 的值即可求得答案
的值即可求得答案
![]() 利用向量的数量积的坐标运算可以求得
利用向量的数量积的坐标运算可以求得![]() ,
,![]() ,利用正弦函数的单调性与最值即可求得
,利用正弦函数的单调性与最值即可求得![]() 的最值和此时
的最值和此时![]() 的值
的值
(1)依题意,tanα=![]() =﹣2,
=﹣2,
∴![]() =
=![]() =
=![]() =﹣10;
=﹣10;
(2)由已知点P的坐标为P(cosθ,sinθ),又![]() =
=![]() +
+![]() ,
,![]() =
=![]() ,
,
∴四边形OAQP为菱形, ∴S=2S△OAP=sinθ, ∵A(1,0),P(cosθ,sinθ),
∴![]() =(1+cosθ,sinθ), ∴
=(1+cosθ,sinθ), ∴![]()
![]() =1+cosθ,
=1+cosθ,
∴f(θ)=(1+cosθ﹣1)2+![]() sinθ﹣1 =cos2θ+
sinθ﹣1 =cos2θ+![]() sinθ﹣1 =﹣sin2θ+
sinθ﹣1 =﹣sin2θ+![]() sinθ,
sinθ,
∵![]() ≤sinθ≤1, ∴当sinθ=
≤sinθ≤1, ∴当sinθ=![]() ,即θ=
,即θ=![]() 时,f(θ)max=
时,f(θ)max=![]() ;
;
当sinθ=1,即θ=![]() 时,f(θ)min=
时,f(θ)min=![]() ﹣1 .
﹣1 .


科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x-1)3-ax-b,x∈R,其中a,b∈R。
(1)求f(x)的单调区间;
(2)若f(x)存在极点x0 , 且f(x1)=f(x0),其中x1≠x0 , 求证:x1+2x0=3;
(3)设a>0,函数g(x)=∣f(x)∣,求证:g(x)在区间[0,2]上的最大值不小于 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)![]() 的部分图象如图所示.
的部分图象如图所示.
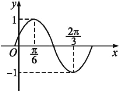
(1)求f(x)的最小正周期及解析式;
(2)设函数g(x)=f(x)-cos 2x,求g(x)在区间![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(![]() sinx-cosx)+m(m∈R),将y=f(x)的图象向左平移
sinx-cosx)+m(m∈R),将y=f(x)的图象向左平移![]() 个单位后得到g(x)的图象,且y=g(x)在区间[
个单位后得到g(x)的图象,且y=g(x)在区间[![]() ]内的最小值为
]内的最小值为![]() .
.
(1)求m的值;
(2)在锐角△ABC中,若g(![]() )=
)=![]() ,求sinA+cosB的取值范围.
,求sinA+cosB的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+![]() }是等比数列.
}是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】铜仁市某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100]分别加以统计,得到如图所示的频率分布直方图.

(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
K2=
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l:x-y-2=0,抛物线C:y2=2px(p>0).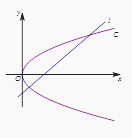
(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证:线段PQ的中点坐标为(2-p , -p);
②求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:x2+y2﹣2ay=0(a>0)截直线x+y=0所得线段的长度是2 ![]() ,则圆M与圆N:(x﹣1)2+(y﹣1)2=1的位置关系是( )
,则圆M与圆N:(x﹣1)2+(y﹣1)2=1的位置关系是( )
A.内切
B.相交
C.外切
D.相离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
(1)证明:A=2B;
(2)若cosB= ![]() ,求cosC的值.
,求cosC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com