科目：高中数学 来源：2017届陕西省宝鸡市高三教学质量检测（一）数学（理）试卷（解析版） 题型：选择题
在等腰直角
中， 
， 
， 
（不与
重合）为
边上的两个动点，且满足
，则
的取值范围为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源：2017届河北省高三下学期二调考试数学（理）试卷（解析版） 题型：填空题
已知是定义在
上的函数，且满足①
；②曲线
关于点
对称；③当
时，
，若
在
上有5个零点，则实数
的取值范围为__________．
查看答案和解析>>
科目：高中数学 来源：2017届贵州省贵阳市高三2月适应性考试（一）数学文试卷（解析版） 题型：解答题
选修4-4：坐标系与参数方程
在直角坐标系中，以坐标原点为极点， 
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为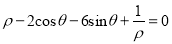
，直线
的参数方程为
（
为参数）.
（1）求曲线
的普通方程；
（2）若直线
与曲线
交于
两点，点
的坐标为
，求
的值.
查看答案和解析>>
科目：高中数学 来源：2017届贵州省贵阳市高三2月适应性考试（一）数学文试卷（解析版） 题型：填空题
我国古代数学家刘徽是公元三世纪世界上最杰出的数学家，他在《九章算术圆田术》注中，用割圆术证明了圆面积的精确公式，并给出了计算圆周率的科学方法.所谓“割圆术”，即通过圆内接正多边形细割圆，并使正多边形的周长无限接近圆的周长，进而来求得较为精确的圆周率（圆周率指圆周长与该圆直径的比率）.刘徽计算圆周率是从正六边形开始的，易知圆的内接正六边形可分为六个全等的正三角形，每个三角形的边长均为圆的半径
，此时圆内接正六边形的周长为
，此时若将圆内接正六边形的周长等同于圆的周长，可得圆周率为3，当用正二十四边形内接于圆时，按照上述算法，可得圆周率为__________．（参考数据： 
）
查看答案和解析>>
科目：高中数学 来源：2017届贵州省贵阳市高三2月适应性考试（一）数学文试卷（解析版） 题型：选择题
下面的程序框图，如果输入三个数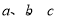
， 
要求判断直线
与单位圆的位置关系，那么在空白的判断框中，应该填入下面四个选项中的（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源：2016-2017学年广东省揭阳市高二下学期第一次阶段考试数学（文）试卷（解析版） 题型：解答题
已知数列
是等比数列，
，
是
和
的等差中项.
（１）求数列
的通项公式；
（２）设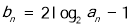
，求数列
的前
项和
．
查看答案和解析>>
科目：高中数学 来源：2016-2017学年广东省揭阳市高二下学期第一次阶段考试数学（文）试卷（解析版） 题型：选择题
设p∶
，q∶
，则
p是q的（ ▲ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
查看答案和解析>>
科目：高中数学 来源：2016-2017学年广东省高二上学期期末考试数学（理）试卷（解析版） 题型：选择题
在三棱柱
中，
是
的中点，
是
的中点，且
，则( )
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
为球的直径，
三点在球面上，且
面
，三角形
，则球的表面积为（ ）
B. 
C. 
D. 
