
| A. | $\frac{1}{3}$ | B. | $\frac{1}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{8}$ |
分析 设送报人到达的时间为x,小明离家的时间为y,则(x,y)可以看成平面中的点,分析可得由试验的全部结果所构成的区域并求出其面积,同理可得事件A所构成的区域及其面积,由几何概型公式,计算可得答案.
解答  解:设送报人到达的时间为x,小明离家的时间为y,记小明离家前能看到报纸为事件A;
解:设送报人到达的时间为x,小明离家的时间为y,记小明离家前能看到报纸为事件A;
以横坐标表示报纸送到时间,以纵坐标表示小明离家时间,建立平面直角坐标系,
小明离家前能得到报纸的事件构成区域如图示:
由于随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.
根据题意,只要点落到阴影部分,就表示小明在离开家前能得到报纸,即事件A发生,
所以P(A)=$\frac{1-\frac{1}{2}×\frac{1}{2}×\frac{1}{2}}{1}$=$\frac{7}{8}$,
故选:D.
点评 本题考查几何概型的计算,解题的关键在于设出x、y,将(x,y)以及事件A在平面直角坐标系中表示出来,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
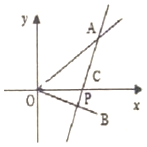 如图,直线OA,OB方程分别为y=x和y=-$\frac{{\sqrt{3}}}{3}$x,过点P(2,0)作直线AB分别交OA,OB于A,B两点,当AB的中点C恰好落在与直线2x+y+m=0,(m∈R)垂直且过原点的直线上时,求直线AB的方程.
如图,直线OA,OB方程分别为y=x和y=-$\frac{{\sqrt{3}}}{3}$x,过点P(2,0)作直线AB分别交OA,OB于A,B两点,当AB的中点C恰好落在与直线2x+y+m=0,(m∈R)垂直且过原点的直线上时,求直线AB的方程.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三人都抽到同一题的概率为$\frac{1}{4}$ | |
| B. | 只有两名女同学抽到同一题的概率为$\frac{1}{4}$ | |
| C. | 其中恰有一男一女抽到同一道题的概率为$\frac{1}{2}$ | |
| D. | 至少有两名同学抽到同一题的概率为$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ω=2,φ=$\frac{π}{2}$ | B. | ω=$\frac{1}{2}$,φ=$\frac{π}{2}$ | C. | ω=$\frac{1}{2}$,φ=$\frac{π}{4}$ | D. | ω=2,φ=$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{2\sqrt{3}}{3}$) | B. | ($\frac{2\sqrt{3}}{3}$,2) | C. | [$\frac{2\sqrt{3}}{3}$,2] | D. | (2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com