
分析 根据对数函数以及二次函数的性质求出使得函数f(x)的定义域是R的a的范围,根据区间长度的比值求出满足条件的概率的值即可.
解答 解:若f(x)=lg(ax2-ax+1)的定义域为R,
则函数g(x)=ax2-ax+1>0恒成立,
a=0时,显然成立,
a≠0时,只需$\left\{\begin{array}{l}{a>0}\\{△{=a}^{2}-4a<0}\end{array}\right.$,
解得:0<a<4,
综上,a∈[0,4),
故满足条件的概率p=$\frac{4}{6}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查了对数函数以及二次函数的性质,考查几何概型问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
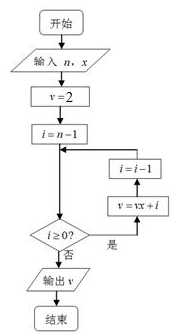 秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )| A. | 66 | B. | 33 | C. | 16 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
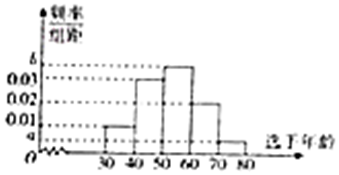 京剧是我国的国粹,是“国家级非物质文化遗产”,为纪念著名京剧表演艺术家、京剧艺术大师梅兰芳先生,某市电视台举办《我爱京剧》的比赛,并随机抽取100位参与《我爱京剧》比赛节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在[30,80]内),样本数据分组区间为[30,40),[40,50),[50,60),[60,70),[70,80],由此得到如图所示的频率分布直方图.
京剧是我国的国粹,是“国家级非物质文化遗产”,为纪念著名京剧表演艺术家、京剧艺术大师梅兰芳先生,某市电视台举办《我爱京剧》的比赛,并随机抽取100位参与《我爱京剧》比赛节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在[30,80]内),样本数据分组区间为[30,40),[40,50),[50,60),[60,70),[70,80],由此得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
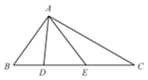 在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )| A. | 31.2 | B. | 32.4 | C. | 33.6 | D. | 34.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>1} | B. | {x|x>0} | C. | {x|0<x<2} | D. | {x|1<x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com