
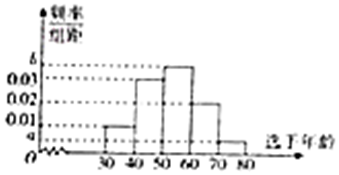
 �������ҹ��Ĺ��⣬�ǡ����Ҽ��������Ļ��Ų�����Ϊ��������������������ҡ�����������ʦ÷����������ij�е���̨�ٰ졶�Ұ����硷�ı������������ȡ100λ���롶�Ұ����硷������Ŀ��Ʊ�ѵ�������Ϊ�������з����о���ȫ��Ʊ�ѵ����䶼��[30��80]�ڣ����������ݷ�������Ϊ[30��40����[40��50����[50��60����[60��70����[70��80]���ɴ˵õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
�������ҹ��Ĺ��⣬�ǡ����Ҽ��������Ļ��Ų�����Ϊ��������������������ҡ�����������ʦ÷����������ij�е���̨�ٰ졶�Ұ����硷�ı������������ȡ100λ���롶�Ұ����硷������Ŀ��Ʊ�ѵ�������Ϊ�������з����о���ȫ��Ʊ�ѵ����䶼��[30��80]�ڣ����������ݷ�������Ϊ[30��40����[40��50����[50��60����[60��70����[70��80]���ɴ˵õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ ������Ƶ�ʷֲ�ֱ��ͼ�������г������飬�����a��b��
������Ƶ�ʷֲ�ֱ��ͼ�����������������[60��70����Ʊ�Ѻ�������[70��80]��Ʊ�����ȡ��������
������������[70��80]���Ʊ����A����[60��70�����Ʊ��Ϊa��b��c��d������г�ȡ���г�ȡ2�˵Ļ����¼�������n=${C}_{5}^{2}$=10�������оٷ�����������������䶼��[60��70���ڵĸ��ʣ�
��� �⣺������Ƶ�ʷֲ�ֱ��ͼ�ã�
$\left\{\begin{array}{l}{��0.01+0.03+b+0.02+a����10=1}\\{0.1��35+0.3��45+10b��55+0.2��65+10a��75=53}\end{array}\right.$��
���a=0.005��b=0.035��
�����ɣ���֪����������[70��80�����Ʊ�ѹ���0.05��100=5�ˣ�
����������[60��70�����Ʊ�ѹ���0.2��100=20�ˣ�
����������[50��60�����Ʊ�ѹ���0.35��100=35�ˣ�
����������[40��50�����Ʊ�ѹ���0.3��100=30�ˣ�
����������[30��40�����Ʊ�ѹ���0.1��100=10�ˣ�
��������[60��70����Ʊ�����ȡ20��$\frac{20}{100}$=4�ˣ�
������[70��80]��Ʊ�����ȡ5��$\frac{20}{100}=1$�ˣ�
������������[70��80]���Ʊ����A����[60��70�����Ʊ��Ϊa��b��c��d��
����г�ȡ���г�ȡ2�˵Ļ����¼�������n=${C}_{5}^{2}$=10��
���������䶼��[60��70���ڵĻ����¼��У�
��a��b������a��c������a��d������b��c������b��d������c��d������6�֣�
���������䶼��[60��70���ڵĸ���P=$\frac{6}{10}=\frac{3}{5}$��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��=2����=$\frac{��}{2}$ | B�� | ��=$\frac{1}{2}$����=$\frac{��}{2}$ | C�� | ��=$\frac{1}{2}$����=$\frac{��}{4}$ | D�� | ��=2����=$\frac{��}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1008 | B�� | 1009 | C�� | 2017 | D�� | 2018 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-4��-1�� | B�� | ��2��4] | C�� | [-4��-1���ȣ�2��4] | D�� | [2��4] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\sqrt{5}$ | C�� | $\sqrt{2}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{15}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{8}{15}$ | D�� | $\frac{7}{30}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2017n-m | B�� | n-2017m | C�� | m | D�� | n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{18}$ | B�� | -$\frac{1}{18}$ | C�� | $\frac{17}{18}$ | D�� | -$\frac{17}{18}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com