
 ,求实数a的取值范围.
,求实数a的取值范围. ,2],不等式f(x)>ax有解,(6分)
,2],不等式f(x)>ax有解,(6分) ,2]的情况.(7分)
,2]的情况.(7分)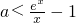 (8分)
(8分) ,则
,则 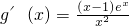
 ,1]内单调递减,在(1,2]内单调递增.
,1]内单调递减,在(1,2]内单调递增. )=2
)=2 -1,
-1, ,且g(2)>g(
,且g(2)>g( )
)
 (12分)
(12分) ≤x≤2}且两个集合的交集不是空集,可转化成,对任意的x∈[
≤x≤2}且两个集合的交集不是空集,可转化成,对任意的x∈[ ,2],不等式f(x)>ax有解,将(1+a)x<ex变形为
,2],不等式f(x)>ax有解,将(1+a)x<ex变形为 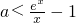 ,令
,令  ,利用导数研究g(x)的最大值,使a小于最大值即可.
,利用导数研究g(x)的最大值,使a小于最大值即可.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com