
科目:高中数学 来源:2015-2016学年江西省赣州市十三县高二上期中联考文科数学试卷(解析版) 题型:选择题
公元前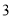 世纪,古希腊欧几里得在《几何原本》里提出:“球的体积(
世纪,古希腊欧几里得在《几何原本》里提出:“球的体积( )与它的直径(
)与它的直径(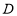 )的立方成正比”,此即
)的立方成正比”,此即 ,欧几里得未给出
,欧几里得未给出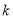 的值.
的值.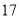 世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式
世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式 中的常数
中的常数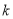 称为“立圆率”或“玉积率
称为“立圆率”或“玉积率 ”.类似地,对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式
”.类似地,对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式 求体
求体 积(在等边圆柱中,
积(在等边圆柱中,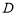 表示底面圆的直径;在正方体中,
表示底面圆的直径;在正方体中,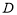 表示棱长).假设运用此体积公式求得球(直径为
表示棱长).假设运用此体积公式求得球(直径为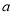 )、等边圆柱(底面圆的直径为
)、等边圆柱(底面圆的直径为 )、正方体(棱长为
)、正方体(棱长为 )的“玉积率”分别为
)的“玉积率”分别为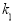 、
、 、
、 ,那么
,那么 ( )
( )
A.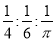 B.
B.
C.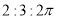 D.
D.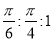
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省赣州市十三县高二上期中联考理科数学试卷(解析版) 题型:选择题
已知点 到直线
到直线 的距离相等,则实数
的距离相等,则实数 的值等于( )
的值等于( )
A. B.
B. C.
C. 或
或 D.
D. 或
或
查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北省宜昌市高二上期中理科数学试卷(解析版) 题型:选择题
△ABC的三个顶点为A(2, 8), B(–4, 0), C(6, 0),则过点B将△ABC的面积平分的直线的方程为( )
A、2x–y+4=0 B、x+2y+4=0
C、2x+y–4=0 D、x–2y+4=0
查看答案和解析>>
科目:高中数学 来源:2016届重庆市高三上学期第三次月考文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4—1:几何证明选讲
如图, 交圆于
交圆于 ,
, 两点,
两点, 切圆于
切圆于 ,
, 为
为 上一点且
上一点且 ,连接
,连接 并延长交圆于点
并延长交圆于点 ,作弦
,作弦 垂直
垂直 ,垂足为
,垂足为 .
.

(1)求证: 为圆的直径;
为圆的直径;
(2)若 ,
,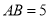 ,求弦
,求弦 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2016届黑龙江省牡丹江市高三上学期期中文科数学试卷(解析版) 题型:解答题
如图,四棱锥 中,
中, ,四边形
,四边形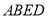 是边长为
是边长为 的正方形,若
的正方形,若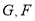 分别是线段
分别是线段 的中点.
的中点.

(1)求证: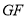 ∥底面
∥底面 ;
;
(2)若点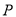 为线段
为线段 的中点,求三角形
的中点,求三角形 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com