
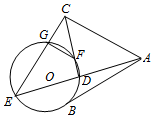
 如图,AB是⊙O的一条切线,切点为B,ADE,CFD,CGE都是⊙O的割线,已知AC=AB.求证:
如图,AB是⊙O的一条切线,切点为B,ADE,CFD,CGE都是⊙O的割线,已知AC=AB.求证:分析 (1)利用切线长与割线长的关系及AB=AC 进行证明.
(2)证明△CAE∽△DAC∽△GCF,得比例式,即可证明结论.
解答 证明:(1)∵AB是⊙O的一条切线,切点为B,ADE,CFD,CGE都是⊙O的割线,
∴AB2=AD•AE,
∵AB=AC,∴AD•AE=AC2.
(2)由(1)有$\frac{AD}{AC}=\frac{AC}{AE}$,
∵∠EAC=∠DAC,
∴△ADC∽△ACE,
∵FG⊥EC,D,E,G,F四点共圆
∴∠ECA=∠CDA=∠CGF=90°,
∵∠CFG=∠CEA
∴△CAE∽△DAC∽△GCF,
∴$\frac{CG}{CF}=\frac{AD}{AC}$,$\frac{CF}{CG}$=$\frac{AE}{AC}$
∴$\frac{CF}{CG}$-$\frac{CG}{CF}$=$\frac{AE}{AC}$-$\frac{AD}{AC}$=$\frac{DE}{AC}$.
点评 本题考查圆的切线、考查三角形相似的判定与性质,考查学生分析解决问题的能力,属于中档题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
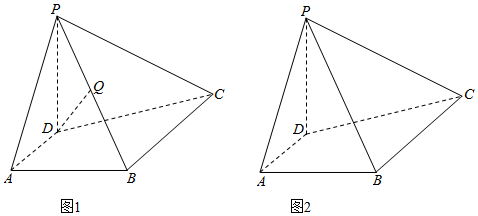
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 倾向“平面几何选讲” | 倾向“坐标系与参数方程” | 倾向“不等式选讲” | 合计 | |
| 男生 | 16 | 4 | 6 | 26 |
| 女生 | 4 | 8 | 12 | 24 |
| 合计 | 20 | 12 | 18 | 50 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
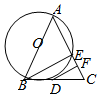 已知:AB为圆O的直径,AB=AC,AC,BC分别交圆O于E,D,连接BE,DF⊥AC于F
已知:AB为圆O的直径,AB=AC,AC,BC分别交圆O于E,D,连接BE,DF⊥AC于F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
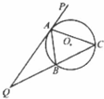 如图,△ABC的外接圆为⊙O,延长CB至Q,再延长QA至P,使得QC2-QA2=BA•QC.
如图,△ABC的外接圆为⊙O,延长CB至Q,再延长QA至P,使得QC2-QA2=BA•QC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com