
分析 (1)运用绝对值不等式的性质:|a|+|b|≥|a-b|,当且仅当ab≤0取得等号,可得f(x)的最小值;
(2)求得f(1),讨论当1-2m<0,当1-2m≥0,去掉绝对值,解m的不等式,即可得到所求m的范围.
解答 解:(1)由m>0,有f(x)=|x+$\frac{8}{m}$|+|x-2m|≥|x+$\frac{8}{m}$-(x-2m)|=|$\frac{8}{m}$+2m|=$\frac{8}{m}$+2m,
当且仅当$({x+\frac{8}{m}})({x-2m})≤0$时,取等号,
所以f(x)的最小值为$\frac{8}{m}+2m$.
(2)f(1)=|1+$\frac{8}{m}$|+|1-2m|(m>0),
当1-2m<0,即$m>\frac{1}{2}$时,$f(1)=1+\frac{8}{m}-({1-2m})=\frac{8}{m}+2m$,
由f(1)>10,得$\frac{8}{m}+2m>10$,化简得m2-5m+4>0,解得m<1或m>4,
所以$\frac{1}{2}<m<1$或m>4;
当1-2m≥0,即$0<m≤\frac{1}{2}$时,$f(1)=1+\frac{8}{m}+({1-2m})=2+\frac{8}{m}-2m$,
由f(1)>10,得$2+\frac{8}{m}-2m>10$,即(m+2)2<8,此式在$0<m≤\frac{1}{2}$时恒成立.
综上,当f(1)>10时,实数m的取值范围是(0,1)∪(4,+∞).
点评 本题考查函数的最值的求法,注意运用绝对值不等式的性质,考查分类讨论的思想方法,化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
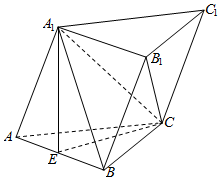 在斜三棱柱ABC-A1B1C1中,底面ABC是正三角形,E是AB中点,A1E⊥平面ABC.
在斜三棱柱ABC-A1B1C1中,底面ABC是正三角形,E是AB中点,A1E⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{2}$ | B. | $\frac{49}{2}$ | C. | 12 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
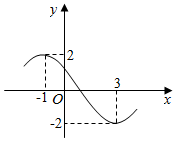
| A. | 0 | B. | 1 | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
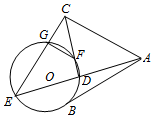 如图,AB是⊙O的一条切线,切点为B,ADE,CFD,CGE都是⊙O的割线,已知AC=AB.求证:
如图,AB是⊙O的一条切线,切点为B,ADE,CFD,CGE都是⊙O的割线,已知AC=AB.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
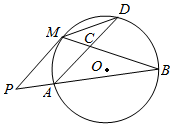 如图,PM是圆O的切线,M为切点,PAB是圆的割线,AD∥PM,点D在圆上,AD与MB交于点C.若AB=6,BC=4,AC=3,则MD等于( )
如图,PM是圆O的切线,M为切点,PAB是圆的割线,AD∥PM,点D在圆上,AD与MB交于点C.若AB=6,BC=4,AC=3,则MD等于( )| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{9}{4}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com