
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市A(看做一点)的东偏南θ角方向 ![]() ,300km的海面P处,并以20km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大.
,300km的海面P处,并以20km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大. 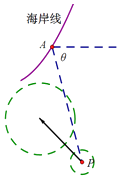
(1)问10小时后,该台风是否开始侵袭城市A,并说明理由;
(2)城市A受到该台风侵袭的持续时间为多久?
【答案】
(1)解:如图建立直角坐标系,
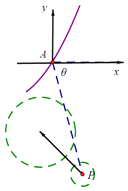
则城市A(0,0),当前台风中心 ![]() ,
,
设t小时后台风中心P的坐标为(x,y),
则 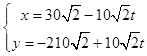 ,此时台风的半径为60+10t,
,此时台风的半径为60+10t,
10小时后,|PA|≈184.4km,台风的半径为r=160km,
∵r<|PA|,
∴10小时后,该台风还没有开始侵袭城市A
(2)解:由(1)知t小时后台风侵袭的范围可视为以 ![]() 为圆心,60+10t为半径的圆,
为圆心,60+10t为半径的圆,
若城市A受到台风侵袭,
则 ![]() ,
,
∴300t2﹣10800t+86400≤0,即t2﹣36t+288≤0,
解得12≤t≤24
∴该城市受台风侵袭的持续时间为12小时.
【解析】(1)建立直角坐标系,,则城市A(0,0),当前台风中心 ![]() ,设t小时后台风中心P的坐标为(x,y),由题意建立方程组,能求出10小时后,该台风还没有开始侵袭城市A.(2)t小时后台风侵袭的范围可视为以
,设t小时后台风中心P的坐标为(x,y),由题意建立方程组,能求出10小时后,该台风还没有开始侵袭城市A.(2)t小时后台风侵袭的范围可视为以 ![]() 为圆心,60+10t为半径的圆,由此利用圆的性质能求出结果.
为圆心,60+10t为半径的圆,由此利用圆的性质能求出结果.


科目:高中数学 来源: 题型:
【题目】已知数列{an}为等比数列,其前n项和为Sn , 则下列结论正确的是( )
A.若a1+a2>0,则a1+a3>0
B.若a1+a3>0,则a1+a2>0
C.若a1>0,则S2017>0
D.若a1>0,则S2016>0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( ) 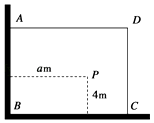
A.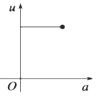
B.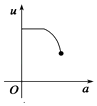
C.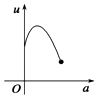
D.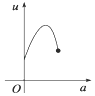
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知曲线 ![]() 及曲线
及曲线 ![]() ,C1上的点P1的横坐标为
,C1上的点P1的横坐标为 ![]() .从C1上的点
.从C1上的点 ![]() 作直线平行于x轴,交曲线C2于Qn点,再从C2上的点
作直线平行于x轴,交曲线C2于Qn点,再从C2上的点 ![]() 作直线平行于y轴,交曲线C1于Pn+1点,点Pn(n=1,2,3…)的横坐标构成数列{an}.
作直线平行于y轴,交曲线C1于Pn+1点,点Pn(n=1,2,3…)的横坐标构成数列{an}. 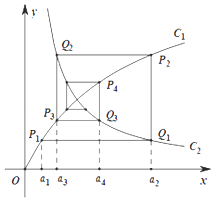
(1)求曲线C1和曲线C2的交点坐标;
(2)试求an+1与an之间的关系;
(3)证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C是平面内到直线l1:x=﹣1和直线l2:y=1的距离之积等于常数k2(k>0)的点的轨迹,下列四个结论:
①曲线C过点(﹣1,1);
②曲线C关于点(﹣1,1)成中心对称;
③若点P在曲线C上,点A、B分别在直线l1、l2上,则|PA|+|PB|不小于2k;
④设P0为曲线C上任意一点,则点P0关于直线l1:x=﹣1,点(﹣1,1)及直线f(x)对称的点分别为P1、P2、P3 , 则四边形P0P1P2P3的面积为定值4k2;其中,
所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则( )
A.乙盒中黑球不多于丙盒中黑球
B.乙盒中红球与丙盒中黑球一样多
C.乙盒中红球不多于丙盒中红球
D.乙盒中黑球与丙盒中红球一样多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x﹣φ)﹣ ![]() sin(2x﹣φ)(|φ|<
sin(2x﹣φ)(|φ|< ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位后关于y轴对称,则f(x)在区间
个单位后关于y轴对称,则f(x)在区间 ![]() 上的最小值为( )
上的最小值为( )
A.﹣1
B.![]()
C.![]()
D.﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com