
分析 由已知条件,得到cos(β-γ)=1+$\frac{3}{2[(k-1)^{2}-1]}$,根据余弦函数和二次函数的性质即可求出最值.
解答 解:cosα+kcosβ+(2-k)cosγ=0,①
sinα+ksinβ+(2-k)sinγ=0,②)
将①②中含有α的项移到右边,得到:kcosβ+(2-k)cosγ=-cosα,③
ksinβ+(2-k)sinγ=-sinα ④,
③④两边分别平方,再左右分别相加(目的是消去α),得到:k2+(2-k)2+2k(2-k)(cosβcosγ+sinβsinγ)=1,
∴2k2-4k+4+2k(2-k)cos(β-γ)=1,
∴cos(β-γ)=$\frac{2{k}^{2}-4k+3}{2{k}^{2}-4k}$=1+$\frac{3}{2{k}^{2}-4k}$=1+$\frac{3}{2[(k-1)^{2}-1]}$,
又0<k<2
当k=1时,(k-1)2-1最小,此时cos(β-γ)最大,cos(β-γ)=-0.5
任意角的余弦最小为-1,当cos(β-γ)=-1,即1+$\frac{3}{2{k}^{2}-4k}$=-1,此时k=$\frac{1}{2}$或$\frac{3}{2}$,
综上,cos(β-γ)最大值为-0.5,最小值为-1
点评 本题考查了三角函数的化简和求值,以及余弦函数的图象和性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=(1,3,5),$\overrightarrow{n}$=(1,0,1) | B. | $\overrightarrow{a}$=(1,0,0),$\overrightarrow{n}$=(-2,0,0) | ||
| C. | $\overrightarrow{a}$=(1,-1,3),$\overrightarrow{n}$=(0,3,1) | D. | $\overrightarrow{a}$=(0,2,1),$\overrightarrow{n}$=(-1,0,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x+1 | B. | $f(x)=-\frac{1}{x}$ | C. | f(x)=x2 | D. | f(x)=x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $2+\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
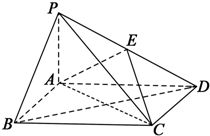 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,$AP=1,AD=\sqrt{3}$,面PAB⊥面ABCD,PA⊥AB,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,$AP=1,AD=\sqrt{3}$,面PAB⊥面ABCD,PA⊥AB,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com