
分析 (1)由曲线C1的极坐标方程ρ2cos2θ=8,曲线C2的极坐标方程为θ=$\frac{π}{6}$,得ρ2cos$\frac{π}{3}$=8,所以ρ2=16,求出ρ,即可求A,B两点的极坐标;
(2)利用参数的几何意义,求线段MN的长度.
解答 解:(1)由曲线C1的极坐标方程ρ2cos2θ=8,曲线C2的极坐标方程为θ=$\frac{π}{6}$,得ρ2cos$\frac{π}{3}$=8,所以ρ2=16,即ρ=±4
所以A,B两点的极坐标为:A(4,$\frac{π}{6}$),B(-4,$\frac{π}{6}$)…(4分)
(2)由曲线C1的极坐标方程得其直角坐标方程为x2-y2=8,…(5分)
将直线$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$代入x2-y2=8整理得t2+2$\sqrt{3}$t-14=0…(6分)
即t1+t2=-2$\sqrt{3}$,t1•t2=-14,…(8分)
所以|MN|=$\sqrt{(-2\sqrt{3})^{2}-4×(-14)}$=2$\sqrt{17}$. …(10分)
点评 本题考查了极坐标与直角坐标的互化公式、此时方程化为普通方程、弦长公式等基础知识与基本技能方法.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
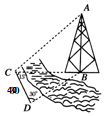 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.测得∠BCD=15°,∠BDC=30°,CD=40米,并在点C测得塔顶A的仰角为60°,则塔高AB=20$\sqrt{6}$米.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D.测得∠BCD=15°,∠BDC=30°,CD=40米,并在点C测得塔顶A的仰角为60°,则塔高AB=20$\sqrt{6}$米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | [-2,2] | C. | (-2,2] | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{14}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | [1,+∞) | C. | (0,2] | D. | (0,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com