
分析 求出函数的导数,通过讨论a的范围,从而求出函数的单调区间即可.
解答 解:y′=x2+2x+a=(x+1)2+a-1,
a≥1时,y′≥0,函数在R递增,
a<1时,令y′>0,解得:x>-1+$\sqrt{1-a}$或x<-1-$\sqrt{1-a}$,
令y′<0,解得:-1-$\sqrt{1-a}$<x<-1+$\sqrt{1-a}$,
∴函数在(-∞,-1-$\sqrt{1-a}$),(-1+$\sqrt{1-a}$,+∞)递增,在(-1-$\sqrt{1-a}$,-1+$\sqrt{1-a}$)递减.
点评 本题考查了函数的单调性问题,考查导数的应用,分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {1,3,4} | C. | {1,4,5} | D. | {2,3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,4} | B. | {1,2,3} | C. | {0,1,2,3,4} | D. | {2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
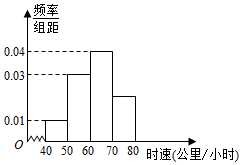 已知某一段公路限速70公里/小时,现抽取400辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这400辆汽车中在该路段超速的有80辆.
已知某一段公路限速70公里/小时,现抽取400辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这400辆汽车中在该路段超速的有80辆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∠BAC=∠B′A′C′ | |
| B. | ∠BAC+∠B′A′C′=180° | |
| C. | ∠BAC=∠B′A′C′或∠BAC+∠B′A′C′=180° | |
| D. | ∠BAC>∠B′A′C′ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com