
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
分析 先根据向量的数量积和向量的垂直求出m的值,再根据充要条件的条件判断即可.
解答 解:非零向量$\overrightarrow a$,$\overrightarrow b$满足$|{\overrightarrow b}|=2|{\overrightarrow a}|$,且$\overrightarrow a$与$\overrightarrow b$的夹角为60°,
由$(\overrightarrow a-m\overrightarrow b)⊥\overrightarrow a$,
∴($\overrightarrow{a}$-m$\overrightarrow{b}$)•$\overrightarrow{a}$=${\overrightarrow{a}}^{2}$-m$\overrightarrow{a}$•$\overrightarrow{b}$=${\overrightarrow{a}}^{2}$-m•2$\overrightarrow{a}$2•cos60°=0,
解得m=1,
∴“m=1”是“$(\overrightarrow a-m\overrightarrow b)⊥\overrightarrow a$”的充要条件,
故选:B
点评 本题考查了向量的数量积和充要条件的定义,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}}]$ | B. | (0,3] | C. | $[{\frac{1}{2},3}]$ | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | 4π | C. | 6π | D. | $\frac{9π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,5} | B. | {2,5,7,8} | C. | {2,3,5,6,7,8} | D. | {1,2,3,4,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
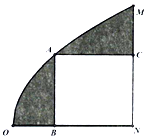 某校一块空地的轮廓线如图所示,曲线段OM是以O为顶点,ON为对称轴且开口向右的抛物线的一段,已知ON=4(单位:百米),MN=4.现计划在该区域内围出一块矩形地块ABNC作为学生活动区域,其余阴影部分进行绿化建设,其中A在曲线段OM上,C在MN上,B在ON上.
某校一块空地的轮廓线如图所示,曲线段OM是以O为顶点,ON为对称轴且开口向右的抛物线的一段,已知ON=4(单位:百米),MN=4.现计划在该区域内围出一块矩形地块ABNC作为学生活动区域,其余阴影部分进行绿化建设,其中A在曲线段OM上,C在MN上,B在ON上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com