
【题目】如图,直三棱柱 ![]() 中,
中, ![]() 分别是
分别是 ![]() 的中点,
的中点, ![]() .
.
(Ⅰ)证明: ![]() ∥平面
∥平面 ![]() ;
;
(Ⅱ)求锐二面角 ![]() 的余弦值.
的余弦值.
【答案】解:
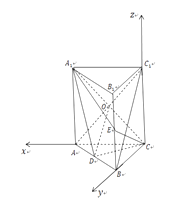
(Ⅰ)连结 ![]() ,交
,交 ![]() 于点
于点 ![]() ,连结
,连结 ![]() ,则
,则 ![]() 为
为 ![]() 的中点,因为
的中点,因为 ![]() 为
为 ![]() 的中点,所以
的中点,所以 ![]() ∥
∥ ![]() ,又因为
,又因为 ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() ∥平面
∥平面 ![]()
(Ⅱ)由 ![]() ,可知
,可知 ![]() ,以
,以 ![]() 为坐标原点,
为坐标原点, ![]() 方向为
方向为 ![]() 轴正方向,
轴正方向, ![]() 方向为
方向为 ![]() 轴正方向,
轴正方向, ![]() 方向为
方向为 ![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系 ![]() ,
,
则 ![]() ,
,
![]() ,
, ![]() ,
, ![]()
设 ![]() 是平面
是平面 ![]() 的法向量,则
的法向量,则 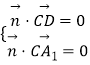 即
即 ![]()
可取 ![]() .
.
同理,设 ![]() 是平面
是平面 ![]() 的法向量,则
的法向量,则 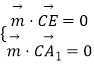 ,
,
可取 ![]() .从而
.从而 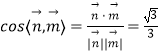
所以锐二面角 ![]() 的余弦值为
的余弦值为 ![]()
【解析】(I)证明线面平行,关键是证明线面平行,因此连结 ![]() ,交
,交 ![]() 于点 O,再利用三角形相似即可。
于点 O,再利用三角形相似即可。
(II)在空间求二面角,我们一般是建系求点,得法向量,再应用夹角公式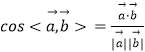 即可。
即可。
【考点精析】利用直线与平面平行的判定对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1曰8日,中共中央、国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值![]() 与这种新材料的含量
与这种新材料的含量![]() (单位:克)的关系为:当
(单位:克)的关系为:当![]() 时,
时, ![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时, ![]() .测得数据如表(部分)
.测得数据如表(部分)
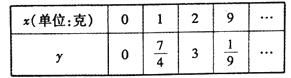
(1)求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(2)其函数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司一年需购买某种原料600吨,设公司每次都购买![]() 吨,每次运费为3万元,一年的总存储费为
吨,每次运费为3万元,一年的总存储费为![]() 万元,一年的总运费与总存储费之和为
万元,一年的总运费与总存储费之和为![]() (单位:万元).
(单位:万元).
(1)试用解析式得![]() 表示成
表示成![]() 的函数;
的函数;
(2)当![]() 为何值时,
为何值时, ![]() 取得最小值?并求出
取得最小值?并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为
是边长为 ![]() 的正方形,
的正方形, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与平面
与平面 ![]() 所成角为
所成角为 ![]() .
.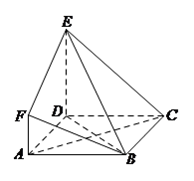
(Ⅰ)求证: ![]() 平面
平面 ![]() .
.
(Ⅱ)求二面角 ![]() 的余弦值.
的余弦值.
(Ⅲ)设点 ![]() 是线段
是线段 ![]() 上一个动点,试确定点
上一个动点,试确定点 ![]() 的位置,使得
的位置,使得 ![]() 平面
平面 ![]() ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合![]() 由满足以下性质的函数
由满足以下性质的函数![]() 组成:①
组成:①![]() 在
在![]() 上是增函数;②对于任意的
上是增函数;②对于任意的![]() ,
, ![]() .已知函数
.已知函数![]() ,
, ![]() .
.
(1)试判断![]() ,
, ![]() 是否属于集合
是否属于集合![]() ,并说明理由;
,并说明理由;
(2)将(1)中你认为属于集合![]() 的函数记为
的函数记为![]() .
.
(ⅰ)试用列举法表示集合![]() ;
;
(ⅱ)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com