
 如图,在三棱锥O-ABC中,三条棱OA,OB,OC两两垂直,且OA>OB>OC,分别经过三条棱OA,OB,OC作一个截面平分三棱锥的体积,截面面积依次为S1,S2,S3,则S1,S2,S3的大小关系为S1>S2>S3.
如图,在三棱锥O-ABC中,三条棱OA,OB,OC两两垂直,且OA>OB>OC,分别经过三条棱OA,OB,OC作一个截面平分三棱锥的体积,截面面积依次为S1,S2,S3,则S1,S2,S3的大小关系为S1>S2>S3. 分析 设OA=a,OB=b,OC=c.过点A,B,C分别作AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D,E,F.由已知利用线面垂直的判定定理可得:OA⊥平面OBC,OA⊥BC,可得BC⊥OD.利用OD=$\frac{OB•OC}{BC}$,可得S1=S△OAD=$\frac{abc}{2\sqrt{{b}^{2}+{c}^{2}}}$.同理可得:S2=$\frac{abc}{2\sqrt{{a}^{2}+{c}^{2}}}$,S3=$\frac{abc}{2\sqrt{{a}^{2}+{b}^{2}}}$.利用a>b>c即可得出大小关系.
解答 解:设OA=a,OB=b,OC=c.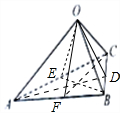
过点A,B,C分别作AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D,E,F.
连接OD,OE,OF,则△OAD,△OBE,△OCF分别为截面.
由已知可得:OA⊥OB,OA⊥OC,OB∩OC=O,∴OA⊥平面OBC,
∴OA⊥BC,又AD∩OA=A,则BC⊥平面OAD,∴BC⊥OD.
∴OD=$\frac{OB•OC}{BC}$=$\frac{bc}{\sqrt{{b}^{2}+{c}^{2}}}$,∴S1=S△OAD=$\frac{1}{2}a•\frac{bc}{\sqrt{{b}^{2}+{c}^{2}}}$=$\frac{abc}{2\sqrt{{b}^{2}+{c}^{2}}}$.
同理可得:S2=$\frac{abc}{2\sqrt{{a}^{2}+{c}^{2}}}$,S3=$\frac{abc}{2\sqrt{{a}^{2}+{b}^{2}}}$.
∵a>b>c,∴$\sqrt{{a}^{2}+{b}^{2}}$$>\sqrt{{a}^{2}+{c}^{2}}$$>\sqrt{{b}^{2}+{c}^{2}}$,
∴$\frac{1}{\sqrt{{a}^{2}+{b}^{2}}}$<$\frac{1}{\sqrt{{a}^{2}+{c}^{2}}}$<$\frac{1}{\sqrt{{b}^{2}+{c}^{2}}}$.
∴S1>S2>S3.
故答案为:S1>S2>S3.
点评 本题考查了线面垂直的判定与性质定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (2)(3) | C. | (3)(4) | D. | (2)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\sqrt{2},\sqrt{2})$ | B. | $(1,\sqrt{2})$ | C. | $(-1,\sqrt{2}]$ | D. | $[1,\sqrt{2})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com