
【题目】在数列![]() 中,若
中,若![]() (
(![]() ,
,![]() ,p为常数),则
,p为常数),则![]() 称为“等方差数列”.下列对“等方差数列”的判断,其中正确的为( )
称为“等方差数列”.下列对“等方差数列”的判断,其中正确的为( )
A.若![]() 是等方差数列,则
是等方差数列,则![]() 是等差数列
是等差数列
B.若![]() 是等方差数列,则
是等方差数列,则![]() 是等方差数列
是等方差数列
C.![]() 是等方差数列
是等方差数列
D.若![]() 是等方差数列,则
是等方差数列,则![]() (
(![]() ,k为常数)也是等方差数列
,k为常数)也是等方差数列
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 所在的半平面和直角梯形
所在的半平面和直角梯形![]() 所在的半平面成
所在的半平面成![]() 的二面角,
的二面角,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
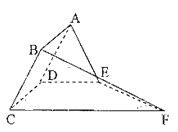
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使锐二面角
,使锐二面角![]() 的余弦值为
的余弦值为![]() .若存在,请求出
.若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的有( )
①在回归分析中,可以借助散点图判断两个变量是否呈线性相关关系.
②在回归分析中,可以通过残差图发现原始数据中的可疑数据,残差平方和越小,模型的拟合效果越好.
③在回归分析模型中,相关系数的绝对值越大,说明模型的拟合效果越好.
④在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 增加0.1个单位.
增加0.1个单位.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年推出一种新型家用轿车,购买时费用为16.9万元,每年应交付保险费、养路费及汽油费共1.2万元,汽车的维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费均比上一年增加0.2万元.
(I)设该辆轿车使用n年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为f(n),求f(n)的表达式;
(II)这种汽车使用多少报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆C的标准方程;
(2)点P是椭圆上异于短轴端点A,B的任意一点,过点P作![]() 轴于Q,线段PQ的中点为M.直线AM与直线
轴于Q,线段PQ的中点为M.直线AM与直线![]() 交于点N,D为线段BN的中点,设O为坐标原点,试判断以OD为直径的圆与点M的位置关系.
交于点N,D为线段BN的中点,设O为坐标原点,试判断以OD为直径的圆与点M的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有大小相同的小球![]() 个,在小球上分别标有1,2,3…,
个,在小球上分别标有1,2,3…,![]() 的号码,已知从盒子中随机取出两个球,两球号码的最大值为
的号码,已知从盒子中随机取出两个球,两球号码的最大值为![]() 的概率为
的概率为![]() .
.
(Ⅰ)盒子中装有几个小球?
(Ⅱ)现从盒子中随机地取出4个球,记所取4个球的号码中,连续自然数的个数的最大值为随机变量![]() (如取标号分别为2,4,6,8的小球时
(如取标号分别为2,4,6,8的小球时![]() ;取标号分别为1,2,4,6的小球时
;取标号分别为1,2,4,6的小球时![]() ;取标号分别为1,2,3,5的小球时
;取标号分别为1,2,3,5的小球时![]() ),求
),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com