
分析 (1)根据$\overrightarrow{m}$•$\overrightarrow{n}$=$\sqrt{3}$列出方程解出A;
(2)使用二倍角公式化简f(x)=-2(sinx-1)2+3,根据二次函数的性质得出f(x)的最值.
解答 解:(Ⅰ)∵$\overrightarrow{m}•\overrightarrow{n}$=$\sqrt{3}$sinA+cosA=2sin(A+$\frac{π}{6}$)=$\sqrt{3}$,
∴$sin(A+\frac{π}{6})=\frac{{\sqrt{3}}}{2}$,
∵A为锐角,∴$A+\frac{π}{6}=\frac{π}{3}$,$A=\frac{π}{6}$.
(Ⅱ)由(Ⅰ)知$sinA=\frac{1}{2}$,
∴f(x)=cos2x+4sinx=1-2sin2x+4sinx=-2(sinx-1)2+3,
∵x∈R,∴sinx∈[-1,1],
∴当sinx=1时,f(x)有最大值3;
当sinx=-1时,f(x)有最小值-5,
∴函数f(x)的值域是[-5,3].
点评 本题考查了三角函数的恒等变换,三角函数化简求值,一元二次函数的最值,属于中档题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{18}{25}$ | B. | $\frac{7}{25}$ | C. | -$\frac{7}{25}$ | D. | -$\frac{16}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
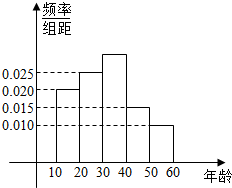 某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.
某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com