
在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为线段BC的中点,E、F为线段AC的三等分点(如图①).将△ABD沿着AD折起到△AB′D的位置,连结B′C(如图②).
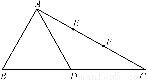
图①

图②
(1)若平面AB′D⊥平面ADC,求三棱锥B′-ADC的体积;
(2)记线段B′C的中点为H,平面B′ED与平面HFD的交线为l,求证:HF∥l;
(3)求证:AD⊥B′E.
(1) (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】(1)解:在直角△ABC中,D为BC的中点,所以AD=BD=CD.又∠B=60°,所以△ABD是等边三角形.取AD中点O,连结B′O,所以B′O⊥AD.因为平面AB′D⊥平面ADC,平面AB′D∩平面ADC=AD,B′O?平面AB′D,所以B′O⊥平面ADC.在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为BC的中点,所以AC=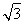 ,B′O=
,B′O=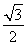 .所以S△ADC=
.所以S△ADC=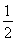 ×
× ×1×
×1×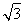 =
=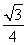 .所以三棱锥B′ADC的体积为V=
.所以三棱锥B′ADC的体积为V=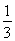 ×S△ADC×B′O=
×S△ADC×B′O= .
.
(2)证明:因为H为B′C的中点,F为CE的中点,所以HF∥B′E.又HF?平面B′ED,B′E?平面B′ED,所以HF∥平面B′ED.因为HF 平面HFD,平面B′ED∩平面HFD=l,所以HF∥l.
平面HFD,平面B′ED∩平面HFD=l,所以HF∥l.
(3)证明:连结EO,由(1)知,B′O⊥AD.
因为AE=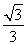 ,AO=
,AO=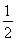 ,∠DAC=30°,
,∠DAC=30°,
所以EO=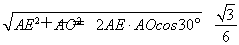 .
.
所以AO2+EO2=AE2.所以AD⊥EO.
又B′O 平面B′EO,EO
平面B′EO,EO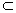 平面B′EO,B′O∩EO=O,
平面B′EO,B′O∩EO=O,
所以AD⊥平面B′EO.
又B′E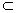 平面B′EO,所以AD⊥B′E.
平面B′EO,所以AD⊥B′E.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第2课时练习卷(解析版) 题型:解答题
设z=2y-2x+4,其中x、y满足条件 求z的最大值和最小值.
求z的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第6课时练习卷(解析版) 题型:解答题
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点.
(1)求二面角D1-AE-C的大小;
(2)求证:直线BF∥平面AD1E.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:解答题
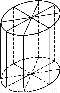
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:填空题
一个圆锥的侧面展开图是圆心角为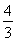 π,半径为18cm的扇形,则圆锥母线与底面所成角的余弦值为________.
π,半径为18cm的扇形,则圆锥母线与底面所成角的余弦值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:填空题
已知正方形ABCD的边长为2,E、F分别为BC、DC的中点,沿AE、EF、AF折成一个四面体,使B、C、D三点重合,则这个四面体的体积为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷(解析版) 题型:解答题
在如图所示的多面体中,已知正三棱柱ABCA1B1C1的所有棱长均为2,四边形ABDC是菱形.
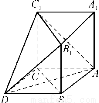
(1)求证:平面ADC1⊥平面BCC1B1;
(2)求该多面体的体积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:解答题
在空间四边形ABCD中,已知AC⊥BD,AD⊥BC,求证:AB⊥CD.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第1课时练习卷(解析版) 题型:填空题
从正方体ABCD-A1B1C1D1的8个顶点中任意取4个不同的顶点,这4个顶点可能是:
(1)矩形的4个顶点;
(2)每个面都是等边三角形的四面体的4个顶点;
(3)每个面都是直角三角形的四面体的4个顶点;
(4)有三个面是等腰直角三角形,有一个面是等边三角形的四面体的4个顶点.
其中正确的结论有________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com