下列函数中.既是偶函数又存在零点的是( )A．y=cos xB．y=sin xC．y=ln xD．y=x2+1 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

2．下列函数中，既是偶函数又存在零点的是（　　）

A．

y=cos x

B．

y=sin x

C．

y=ln x

D．

y=x²+1

分析利用函数奇偶性的判断方法以及零点的判断方法对选项分别分析选择．

解答解：对于A，定义域为R，并且cos（-x）=cosx，是偶函数并且有无数个零点；
对于B，sin（-x）=-sinx，是奇函数，由无数个零点；
对于C，定义域为（0，+∞），所以是非奇非偶的函数，有一个零点；
对于D，定义域为R，为偶函数，没有零点；
故选A．

点评本题考查了函数的奇偶性和零点的判断．①求函数的定义域；②如果定义域关于原点不对称，函数是非奇非偶的函数；如果关于原点对称，再判断f（-x）与f（x）的关系；相等是偶函数，相反是奇函数；函数的零点与函数图象与x轴的交点以及与对应方程的解的个数是一致的．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

12．椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$的两个焦点为F₁，F₂，过F₁的直线交椭圆于A、B两点，若|AB|=6，则|AF₂|+|BF₂|的值为（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

13．等差数列{a_n}的前n项和为S_n，已知（a₁₀₀₇-1）³+2 015（a₁₀₀₇-1）=1，（a₁₀₀₉-1）³+2 015（a₁₀₀₉-1）=-1，则（　　）

	A．	S₂₀₁₅=2 015，a₁₀₀₉＞1＞a₁₀₀₇		B．	S₂₀₁₅=2 015，a₁₀₀₇＞1＞a₁₀₀₉
	C．	S₂₀₁₅=-2 015，a₁₀₀₉＞1＞a₁₀₀₇		D．	S₂₀₁₅=-2 015，a₁₀₀₇＞1＞a₁₀₀₉

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

10．已知{a_n}为等比数列，若a₄+a₆=8，则a₁a₇+2a₃a₇+a₃a₉=64．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

17．已知抛物线x²=4y的焦点为F，P为该抛物线上的一个动点．
（1）当|PF|=2时，求点P的坐标；
（2）过F且斜率为1的直线与抛物线交与两点AB，若P在弧AB上，求△PAB面积的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

7．

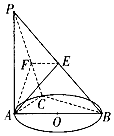如图所示，PA垂直于圆O所在平面，AB是圆O的直径，C是圆O上一点，点A在PB，PC上的射影分别为E，F，则以下结论错误的是（　　）

A．

PB⊥AF

B．

PB⊥EF

C．

AF⊥BC

D．

AE⊥BC

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

14．在四棱锥P-ABCD中，底面ABCD是一直角梯形，BA⊥AD，AD∥BC，AB=BC=2，PA=3，AD=6，PA⊥底面ABCD，E是PD上的动点．若CE∥平面PAB，则三棱锥C-ABE的体积为（　　）

A．

$\frac{1}{2}$

B．

$\frac{2}{3}$

C．

$\frac{3}{2}$

D．

$\frac{4}{3}$

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．已知约束条件$\left\{\begin{array}{l}{x+y-3≥0}\\{x-2y+3≥0}\\{x≤a}\end{array}\right.$，表示的可行域为D，其中a＞1，点（x₀，y₀）∈D，点（m，n）∈D．若3x₀-y₀与$\frac{n+1}{m}$的最小值相等，则实数a等于（　　）

A．

$\frac{5}{4}$

B．

$\frac{3}{2}$

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．快递员通知小张中午12点到小区门口取快递，由于工作原因，快递员于11：50到12：10之间随机到达小区门口，并停留等待10分钟，若小张于12：00到12：10之间随机到达小区门口，也停留等待10分钟，则小张能取到快递的概率为（　　）

A．

$\frac{1}{2}$

B．

$\frac{7}{12}$

C．

$\frac{2}{3}$

D．

$\frac{3}{4}$

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学