
分析 求导数,确定函数的单调性,即可求函数f(x)的值域;g(x)∈(0,e],分类讨论,研究f(x)的单调性,即可求a的取值范围.
解答 解:g′(x)=$\frac{e(1-x)}{{e}^{x}}$,令$\frac{e(1-x)}{{e}^{x}}$=0,解得x=1,
∵ex>0,∴x∈(0,1)时,g′(x)>0;x∈(1,e]时,g′(x)<0,g(x)在(0,1]上单调递增,在(1,e]单调单调递减,根据极大值的定义知:g(x)极大值是g(1)=1,又g(0)=0,g(e)=$\frac{{e}^{2}}{{e}^{e}}$,所以g(x)的值域是(0,1].
函数f(x)=a(x-1)2-lnx,x>0,f′(x)=2ax-2a-$\frac{1}{x}$=$\frac{2{ax}^{2}-2ax-1}{x}$,
令h(x)=2ax2-2ax-1,h(x)恒过(0,-1),
当a=0时,f′(x)<0,f(x)是减函数,不满足题意.
h(x)=0,可得2ax2-2ax-1=0,△=4a2+8a,△>0解得a<-2或a>0.
当-2<a<0时,h(x)的对称轴为:x=$\frac{1}{2}$,h(x)<0恒成立,f′(x)<0,f(x)是减函数,不满足题意.
当a<-2时,x∈(0,$\frac{a-\sqrt{{a}^{2}+2a}}{2a}$),h(x)<0恒成立,f′(x)<0,f(x)是减函数,
x∈$(\frac{a-\sqrt{{a}^{2}+2a}}{2a},\frac{a+\sqrt{{a}^{2}+2a}}{2a})$,f′(x)>0,f(x)是增函数,x∈$(\frac{a+\sqrt{{a}^{2}+2a}}{2a},e)$,f′(x)<0,f(x)是减函数,
若对任意的x0∈(0,e],总存在两个不同的x1,x2∈(0,e],使得f(x1)=f(x2)=g(x0).
可知f(x)极大值≥1,f(x)极小值≤0.可得$\left\{\begin{array}{l}f(\frac{a+\sqrt{{a}^{2}+2a}}{2a})≥1\\ f(e)≤0\\ f(\frac{a-\sqrt{{a}^{2}+2a}}{2a})≤0\end{array}\right.$,$\left\{\begin{array}{l}{f(\frac{a+\sqrt{{a}^{2}+2a}}{2a})≥1}\\{f(e)≤0或f(\frac{a-\sqrt{{a}^{2}+2a}}{2a})≤0}\end{array}\right.$,
∵f(x)=a(x-1)2-lnx,$a(\frac{a+\sqrt{{a}^{2}+2a}}{2a}{-1)}^{2}-ln\frac{a+\sqrt{{a}^{2}+2a}}{2a}≥1$,不等式不成立.
当a>0时,x∈(0,$\frac{a+\sqrt{{a}^{2}+2a}}{2a}$),h(x)<0恒成立,f′(x)<0,f(x)是减函数,
x∈$(\frac{a+\sqrt{{a}^{2}+2a}}{2a},e)$,f′(x)>0,f(x)是增函数,因为x=1时,f(1)=0,只需f(e)≥1.
可得:a(e-1)2-1≥1,
解得a≥$\frac{2}{(e-1)^{2}}$.
综上:实数a的取值范围为:a≥$\frac{2}{(e-1)^{2}}$.
点评 本题考查函数的导数的综合应用,考查函数的最值,考查分类讨论思想以及转化思想的应用.难度比较大.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:选择题
| A. | [-2,6] | B. | (-6,1) | C. | (-6,2) | D. | (-4,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{2,\frac{5}{2}}]$ | B. | $[{\frac{5}{4},\frac{5}{2}}]$ | C. | $[{\frac{4}{5},\frac{5}{2}}]$ | D. | $[{\frac{5}{4},2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
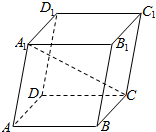 如图所示的平行六面体ABCD-A1B1C1D中,AB=AD=AA1=1,∠BAD=90°,∠BAA1=∠DAA1=60°,则CA1的长=1.
如图所示的平行六面体ABCD-A1B1C1D中,AB=AD=AA1=1,∠BAD=90°,∠BAA1=∠DAA1=60°,则CA1的长=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com