
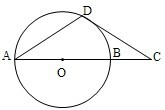
 ±¾Ìâ°üÀ¨A¡¢B¡¢C¡¢DËÄСÌ⣬ÇëÑ¡¶¨ÆäÖÐÁ½Ì⣬²¢ÔÚÏàÓ¦µÄ´ðÌâÇøÓòÄÚ×÷´ð£®Èô¶à×ö£¬Ôò°´×÷´ðµÄÇ°Á½ÌâÆÀ·Ö£®½â´ðʱӦд³öÎÄ×Ö˵Ã÷¡¢Ö¤Ã÷¹ý³Ì»òÑÝËã²½Ö裮
±¾Ìâ°üÀ¨A¡¢B¡¢C¡¢DËÄСÌ⣬ÇëÑ¡¶¨ÆäÖÐÁ½Ì⣬²¢ÔÚÏàÓ¦µÄ´ðÌâÇøÓòÄÚ×÷´ð£®Èô¶à×ö£¬Ôò°´×÷´ðµÄÇ°Á½ÌâÆÀ·Ö£®½â´ðʱӦд³öÎÄ×Ö˵Ã÷¡¢Ö¤Ã÷¹ý³Ì»òÑÝËã²½Ö裮
|
|
| ab |
|
|
|
| ab |
| a |
| a |
| b |
| b |
| b |
| a |
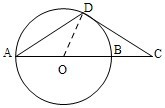
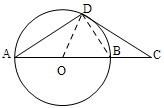
|
|
|
|
|
|
| |3•1+4•0+a| | ||
|
| ab |
| a |
| a |
| b |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| ab |
| ab |
| a |
| a |
| b |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| ab |



| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º
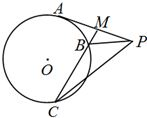 Ñ¡×öÌâ±¾Ìâ°üÀ¨A£¬B£¬C£¬DËÄСÌ⣬ÇëÑ¡¶¨ÆäÖÐ Á½Ìâ ×÷´ð£¬Ã¿Ð¡Ìâ10·Ö£¬¹²¼Æ20·Ö£¬
Ñ¡×öÌâ±¾Ìâ°üÀ¨A£¬B£¬C£¬DËÄСÌ⣬ÇëÑ¡¶¨ÆäÖÐ Á½Ìâ ×÷´ð£¬Ã¿Ð¡Ìâ10·Ö£¬¹²¼Æ20·Ö£¬
|
|
|
|
| ¦Ð |
| 4 |
| 2 |
| 1 |
| 3a+2 |
| 1 |
| 3b+2 |
| 1 |
| 3c+2 |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º
 £¨2013•ËÞǨһģ£©¡¾Ñ¡×öÌâ¡¿±¾Ìâ°üÀ¨A¡¢B¡¢C¡¢DËÄСÌ⣬ÇëÑ¡¶¨ÆäÖÐÁ½Ì⣬²¢ÔÚÏàÓ¦µÄ´ðÌâÇøÓòÄÚ×÷´ð£®Èô¶à×ö£¬Ôò°´×÷´ðµÄÇ°Á½ÌâÆÀ·Ö£®½â´ðʱӦд³öÎÄ×Ö˵Ã÷¡¢Ö¤Ã÷¹ý³Ì»òÑÝËã²½Ö裮
£¨2013•ËÞǨһģ£©¡¾Ñ¡×öÌâ¡¿±¾Ìâ°üÀ¨A¡¢B¡¢C¡¢DËÄСÌ⣬ÇëÑ¡¶¨ÆäÖÐÁ½Ì⣬²¢ÔÚÏàÓ¦µÄ´ðÌâÇøÓòÄÚ×÷´ð£®Èô¶à×ö£¬Ôò°´×÷´ðµÄÇ°Á½ÌâÆÀ·Ö£®½â´ðʱӦд³öÎÄ×Ö˵Ã÷¡¢Ö¤Ã÷¹ý³Ì»òÑÝËã²½Ö裮| 5 |
|
|
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º
 Ñ¡×÷Ì⣬±¾Ìâ°üÀ¨A¡¢B¡¢C¡¢DËÄСÌ⣬ÇëÑ¡¶¨ÆäÖÐÁ½Ì⣬²¢ÔÚÏàÓ¦µÄ´ðÌâÇøÓòÄÚ×÷´ð£®Èô¶à×ö£¬Ôò°´×÷´ðµÄÇ°Á½ÌâÆÀ·Ö£®½â´ðʱӦд³öÎÄ×Ö˵Ã÷¡¢Ö¤Ã÷¹ý³Ì»òÑÝËã²½Ö裮
Ñ¡×÷Ì⣬±¾Ìâ°üÀ¨A¡¢B¡¢C¡¢DËÄСÌ⣬ÇëÑ¡¶¨ÆäÖÐÁ½Ì⣬²¢ÔÚÏàÓ¦µÄ´ðÌâÇøÓòÄÚ×÷´ð£®Èô¶à×ö£¬Ôò°´×÷´ðµÄÇ°Á½ÌâÆÀ·Ö£®½â´ðʱӦд³öÎÄ×Ö˵Ã÷¡¢Ö¤Ã÷¹ý³Ì»òÑÝËã²½Ö裮
|
|
|
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖÐÊýѧ À´Ô´£º ÌâÐÍ£º
 Ñ¡×÷Ì⣬±¾Ìâ°üÀ¨A¡¢B¡¢C¡¢DËÄСÌ⣬ÇëÑ¡¶¨ÆäÖÐÁ½Ì⣬²¢ÔÚÏàÓ¦µÄ´ðÌâÇøÓòÄÚ×÷´ð£®Èô¶à×ö£¬Ôò°´×÷´ðµÄÇ°Á½ÌâÆÀ·Ö£®½â´ðʱӦд³öÎÄ×Ö˵Ã÷¡¢Ö¤Ã÷¹ý³Ì»òÑÝËã²½Ö裮
Ñ¡×÷Ì⣬±¾Ìâ°üÀ¨A¡¢B¡¢C¡¢DËÄСÌ⣬ÇëÑ¡¶¨ÆäÖÐÁ½Ì⣬²¢ÔÚÏàÓ¦µÄ´ðÌâÇøÓòÄÚ×÷´ð£®Èô¶à×ö£¬Ôò°´×÷´ðµÄÇ°Á½ÌâÆÀ·Ö£®½â´ðʱӦд³öÎÄ×Ö˵Ã÷¡¢Ö¤Ã÷¹ý³Ì»òÑÝËã²½Ö裮
|
| x2 |
| 12 |
| y2 |
| 4 |
²é¿´´ð°¸ºÍ½âÎö>>
¹ú¼ÊѧУÓÅÑ¡ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com