
【题目】下列命题中正确命题的序号是( )
①函数f(x)在定义域R内可导,“f′(1)=0”是“函数f(x)在x=1处取极值”的充分不必要条件;
②函数f(x)=x3![]() ax在[1,2]上单调递增,则a≥﹣4
ax在[1,2]上单调递增,则a≥﹣4
③在一次射箭比赛中,甲、乙两名射箭手各射箭一次.设命题p:“甲射中十环”,命题q:“乙射中十环”,则命题“至少有一名射箭手没有射中十环”可表示为(¬p)∨(¬q);
④若椭圆![]() 左、右焦点分别为F1,F2,垂直于x轴的直线交椭圆于A,B两点,当直线过右焦点时,△ABF1的周长取最大值
左、右焦点分别为F1,F2,垂直于x轴的直线交椭圆于A,B两点,当直线过右焦点时,△ABF1的周长取最大值
A.①③④B.②③④C.②③D.①④
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,圆
,圆![]() 与圆
与圆![]() 关于直线
关于直线![]() :
:![]() 对称.
对称.
(1)求圆![]() 的方程;
的方程;
(2)过直线![]() 上的点
上的点![]() 分别作斜率为
分别作斜率为![]() ,4的两条直线
,4的两条直线![]() ,
,![]() ,求使得
,求使得![]() 被圆
被圆![]() 截得的弦长与
截得的弦长与![]() 被圆
被圆![]() 截得的弦长相等时点
截得的弦长相等时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天坛公园是明、清两代皇帝“祭天”“祈谷”的场所.天坛公园中的圜丘台共有三层(如图1所示),上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石(如图2所示).上层坛从第一环至第九环共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则第二十七环的扇面形石块数是______;上、中、下三层坛所有的扇面形石块数是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂有方木料90![]() ,五合板600
,五合板600![]() ,准备加工成书桌和书橱出售.已知生产第张书桌需要方木料O.l
,准备加工成书桌和书橱出售.已知生产第张书桌需要方木料O.l![]() ,五合板2
,五合板2![]() ,生产每个书橱而要方木料0.2
,生产每个书橱而要方木料0.2![]() ,五合板1
,五合板1![]() ,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
(1)如果只安排生产书桌,可获利润多少?
(2)怎样安排生产可使所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法中正确的有______.(填序号)①数据2,2,3,3,4,6,7,3的众数与中位数相等;②数据1,3,5,7,9的方差是数据2,6,10,14,18的方差的一半;③一组数据的方差大小反映该组数据的波动性,若方差越大,则波动性越大,方差越小,则波动性越小.④频率分布直方图中各小长方形的面积等于相应各组的频数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】顺次连接椭圆![]() 的四个顶点恰好构成了一个边长为
的四个顶点恰好构成了一个边长为![]() 且面积为
且面积为![]() 的菱形。
的菱形。
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个不同点,若直线
上的两个不同点,若直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() (以
(以![]() 为坐标原点),线段
为坐标原点),线段![]() 上有一点
上有一点![]() 满足
满足![]() ,连接并延长交椭圆
,连接并延长交椭圆![]() 于点
于点![]() ,求椭圆
,求椭圆![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an} 满足a1=a,![]() =can+1﹣c(n∈N*),其中a、c为实数,且c≠0.
=can+1﹣c(n∈N*),其中a、c为实数,且c≠0.
(1)求数列{an} 的通项公式;
(2)设a=![]() ,c=
,c=![]() ,bn=n(1﹣an)(n∈N*),求数列 {bn}的前n项和Sn.
,bn=n(1﹣an)(n∈N*),求数列 {bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABC-A1B1C1中,底面ABC是边长为2的等边三角形,上、下底面的面积之比为1:4,侧面A1ABB1⊥底面ABC,并且A1A=A1B1,∠AA1B=90°.
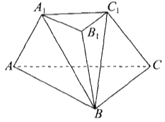
(1)平面A1C1B∩平面ABC=l,证明:A1C1∥l;
(2)求四棱锥B-A1ACC1的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com