
【题目】已知函数![]() ,函数
,函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)设函数![]() (
(![]()
![]() ),讨论
),讨论![]() 的单调性;
的单调性;
(3)若对任意![]() ,恒有关于
,恒有关于![]() 的不等式
的不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() .(2)答案见解析.(3)
.(2)答案见解析.(3)![]()
【解析】
(1)由函数![]() ,求导得到
,求导得到![]() , 再求得
, 再求得![]() ,
,![]() ,写出切线方程.
,写出切线方程.
(2)易得![]()
![]()
![]() ,由
,由![]() 在
在![]()
![]() 上恒成立,根据
上恒成立,根据![]() ,分
,分![]() ,
,![]() 讨论求解.
讨论求解.
(3)根据对任意![]() ,恒有关于
,恒有关于![]() 的不等式
的不等式![]() 成立,转化为
成立,转化为![]() ,对任意
,对任意![]() 恒成立,设
恒成立,设![]() (
(![]() ,用导数法求其最小值即可.
,用导数法求其最小值即可.
(1)因为![]()
所以![]() ,
,
所以![]() .
.
因为![]() ,
,
所以![]() ,
,
即所求曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(2)易知,函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
且有![]()
![]()
![]() .
.
因为![]() 在
在![]()
![]() 上恒成立,
上恒成立,
所以①当![]() 时,
时,![]() 在
在![]()
![]() 上恒成立,此时
上恒成立,此时![]() ,
,
所以,![]() 在区间
在区间![]() 上单调递增.
上单调递增.
②当![]() 时,由
时,由![]() ,即
,即![]() ,解得
,解得![]() ;
;
由![]() ,即
,即![]() ,解得
,解得![]() .
.
所以,![]() 在区间
在区间![]() 上单调递减;
上单调递减;
在区间![]() 上单调递增.
上单调递增.
(3)因为对任意![]() ,恒有关于
,恒有关于![]() 的不等式
的不等式![]() 成立,
成立,
所以 ![]() ,对任意
,对任意![]() 恒成立,
恒成立,
设![]() (
(![]() ).
).
易得![]() ,
,![]() .
.
令![]() ,
,![]() ,
,
所以![]() .
.
显然,当![]() 时,
时,![]() 恒成立.
恒成立.
所以函数![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,
,
即![]() 在
在![]() 恒成立.
恒成立.
所以,函数![]() 在
在![]()
![]() 单调递减.
单调递减.
所以有![]() ,
,
所以![]() .
.
故所求实数![]() 的取值范围是
的取值范围是![]() .
.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)为奇函数,且当x≥0时,f(x)=ex﹣cosx,则不等式f(2x﹣1)+f(x﹣2)>0的解集为( )
A.(﹣∞,1)B.(﹣∞,![]() )C.(
)C.(![]() ,+∞)D.(1,+∞)
,+∞)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有四大国粹:京剧、武术、中医和书法.某大学开设这四门课供学生选修,男生甲选其中三门课进行学习,已知他选修了京剧,则他选修书法的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有教师400人,其中高中教师240人.为了了解该校教师每天课外锻炼时间,现利用分层抽样的方法从该校教师中随机抽取了100名教师进行调查,统计其每天课外锻炼时间(所有教师每天课外锻炼时间均在![]() 分钟内),将统计数据按
分钟内),将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分成6组,制成频率分布直方图如下:假设每位教师每天课外锻炼时间相互独立,并称每天锻炼时间小于20分钟为缺乏锻炼.
分成6组,制成频率分布直方图如下:假设每位教师每天课外锻炼时间相互独立,并称每天锻炼时间小于20分钟为缺乏锻炼.
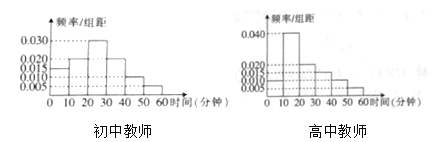
(1)试估计本校教师中缺乏锻炼的人数;
(2)从全市高中教师中随机抽取3人,若![]() 表示每天课外锻炼时间少于10分钟的人数,以这60名高中教师每天课外锻炼时间的频率代替每名高中教师每天课外锻炼时间发生的概率,求随机变量
表示每天课外锻炼时间少于10分钟的人数,以这60名高中教师每天课外锻炼时间的频率代替每名高中教师每天课外锻炼时间发生的概率,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】角谷猜想,也叫![]() 猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1.如:取
猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1.如:取![]() ,根据上述过程,得出6,3,10,5,16,8,4,2,1,共9个数.若
,根据上述过程,得出6,3,10,5,16,8,4,2,1,共9个数.若![]() ,根据上述过程得出的整数中,随机选取两个不同的数,则这两个数都是偶数的概率为( )
,根据上述过程得出的整数中,随机选取两个不同的数,则这两个数都是偶数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考取消文理科,实行“3+3”,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人(把年龄在[15,45)称为中青年,年龄在[45,75)称为中老年),并把调查结果制成如表:

(1)请根据上表完成下面2×2列联表,并判断是否有95%的把握认为对新高考的了解与年龄(中青年、中老年)有关?
附:K2![]() .
.

(2)现采用分层抽样的方法从中老年人中抽取8人,再从这8人中随机抽取2人进行深入调查,求事件A:“恰有一人年龄在[45,55)”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:存在
满足:存在![]() ,对任意的
,对任意的![]() ,都有
,都有![]() (
(![]() 为常数),则称
为常数),则称![]() 具有性质
具有性质![]()
(1)若无穷数列![]() 具有性质
具有性质![]() ,且
,且![]() ,求
,求![]() 的值
的值
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列,![]() ,
,![]() ,
,![]() ,判断
,判断![]() 是否具有性质
是否具有性质![]() ,并说明理由.
,并说明理由.
(3)设无穷数列![]() 既具有性质
既具有性质![]() ,又具有性质
,又具有性质![]() ,其中
,其中![]() 互质,求证:数列
互质,求证:数列![]() 具有性质
具有性质![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(0,2),B(0,﹣2),动点P(x,y)满足PA,PB的斜率之积为![]() .
.
(1)求动点P的轨迹C的方程;
(2)已知直线l:y=kx+m,C的右焦点为F,直线l与C交于M,N两点,若F是△AMN的垂心,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com