
| A. |  | B. |  | C. |  | D. |  |
分析 作出不等式组对应的平面区域,利用分类讨论分别求出当t取不同值时,对应区域的面积,利用函数的性质进行判断即可.
解答 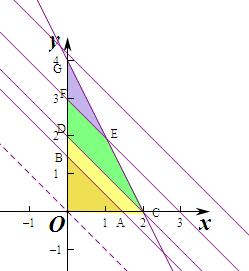 解:作出不等式组对应的平面区域如图,
解:作出不等式组对应的平面区域如图,
当直线y+x=t经过C(2,0)时,此时t=2,
即当0<t≤2时,阴影部分为三角形OAB,
此时A(t,0),B(0,t),
则平面区域的面积为S(t)=$\frac{1}{2}$t2,为开口向上的抛物线的一段,
当直线y+x=t经过G(0,4)时,此时t=4,
当t≥4时,对应的区域为三角形OCG,此时G(0,4),C(2,0),
此时三角形的面积为S(t)=$\frac{1}{2}$×2×4=4为定值,排除B,D,
当2<t<4时,此时平面区域为四边形OCEF,
此时F(0,t),
由$\left\{\begin{array}{l}{x+y=t}\\{y+2x=4}\end{array}\right.$得$\left\{\begin{array}{l}{x=4-t}\\{y=2t-4}\end{array}\right.$,即E(4-t,2t-4),
此时四边形OCEF的面积S=S△OCG-S△GFE=4-$\frac{1}{2}$(4-t)(4-t)=4-$\frac{1}{2}$(t-4)2,为开口向下的抛物线,
故选:A
点评 本题主要考查线性规划的应用,考查函数作图的能力,作出不等式组对应的平面区域,求出对应的区域以及对应的区域的面积是解决本题的关键.注意要进行分类讨论.


科目:高中数学 来源: 题型:解答题
 如图,点A,B,C是椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的三个顶点,D是OA的中点,P、Q是直线x=4上的两个动点.
如图,点A,B,C是椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的三个顶点,D是OA的中点,P、Q是直线x=4上的两个动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知直线l:y=kx+1与椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<2).
已知直线l:y=kx+1与椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
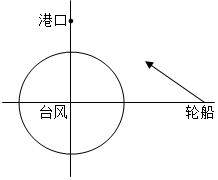 一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西60km处,受影响的范围是半径长为20km的圆形区域.已知港口位于台风中心正北30km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西60km处,受影响的范围是半径长为20km的圆形区域.已知港口位于台风中心正北30km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com