
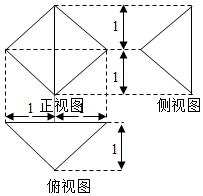
分析 由三视图知几何体是一个三棱锥,在对应的正方体中作出此三棱锥,利用正方体的长度和位置关系求出各个棱长,利用分割法和椎体的体积公式求出此三棱锥的体积.
解答 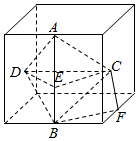 解:由三视图知几何体是一个三锥A-BCD,如图:
解:由三视图知几何体是一个三锥A-BCD,如图:
图中的正方体的棱长是2,其中A、B、E、F分别是对应边的中点,C、D是对应面的中心,
由图得,AB⊥平面CDE,AB=CD=2,CF=AE=BE=1,
又BF=$\sqrt{2}$,则BC=$\sqrt{{1}^{2}+(\sqrt{2})^{2}}$=$\sqrt{3}$,
即AD=BD=AC=BC=$\sqrt{3}$
所以棱锥的各棱长之和:4+4$\sqrt{3}$,
又DE=EC=BF=$\sqrt{2}$,CD=2,
所以几何体的体积V=VA-DEC+VB-DEC=2×$\frac{1}{3}•{S}_{△DEC}•AE$
=2×$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{2}×1$=$\frac{2}{3}$,
故答案为:$4+4\sqrt{3},\frac{2}{3}$.
点评 本题考查三视图求几何体的体积和棱长,此几何体放在正方体中直观、容易理解,由三视图正确复原几何体是解题的关键,考查空间想象能力和转化能力.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
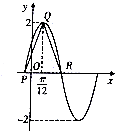 函数f(x)=2sin(ωx+φ)(?>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图所示.,若$\overrightarrow{PQ}$•$\overrightarrow{QR}$=$\frac{{π}^{2}}{16}$-4,为了得到函数f(x)的图象只要把函数y=2sinx图象上所有的点( )
函数f(x)=2sin(ωx+φ)(?>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图所示.,若$\overrightarrow{PQ}$•$\overrightarrow{QR}$=$\frac{{π}^{2}}{16}$-4,为了得到函数f(x)的图象只要把函数y=2sinx图象上所有的点( )| A. | 横坐标缩短到原来的$\frac{1}{2}$倍,纵坐标不变,再向左平移$\frac{π}{3}$个单位 | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$倍,纵坐标不变,再向左平移$\frac{π}{6}$个单位 | |
| C. | 横坐标伸长到原来的2倍,纵坐标不变,再向左平移$\frac{π}{3}$个单位 | |
| D. | 横坐标伸长到原来的2倍,纵坐标不变,再向左平移$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向右平移$\frac{π}{2}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
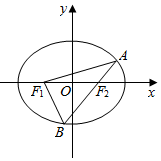 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1(-1,0),F2(1,0),离心率为$\frac{\sqrt{2}}{2}$.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1(-1,0),F2(1,0),离心率为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com