
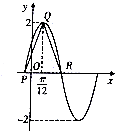
 函数f(x)=2sin(ωx+φ)(?>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图所示.,若$\overrightarrow{PQ}$•$\overrightarrow{QR}$=$\frac{{π}^{2}}{16}$-4,为了得到函数f(x)的图象只要把函数y=2sinx图象上所有的点( )
函数f(x)=2sin(ωx+φ)(?>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图所示.,若$\overrightarrow{PQ}$•$\overrightarrow{QR}$=$\frac{{π}^{2}}{16}$-4,为了得到函数f(x)的图象只要把函数y=2sinx图象上所有的点( )| A. | 横坐标缩短到原来的$\frac{1}{2}$倍,纵坐标不变,再向左平移$\frac{π}{3}$个单位 | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$倍,纵坐标不变,再向左平移$\frac{π}{6}$个单位 | |
| C. | 横坐标伸长到原来的2倍,纵坐标不变,再向左平移$\frac{π}{3}$个单位 | |
| D. | 横坐标伸长到原来的2倍,纵坐标不变,再向左平移$\frac{π}{6}$个单位 |
分析 利用直角三角形中的边角关系、余弦定理求出周期T,再由周期求出ω,由五点法作图求出φ的值,可得f(x)的解析式,再利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:根据函数f(x)=2sin(ωx+φ)(?>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象,可得PQ=QR=$\sqrt{{(\frac{T}{4})}^{2}{+2}^{2}}$,
cos$\frac{∠PQR}{2}$=$\frac{2}{\sqrt{\frac{{T}^{2}}{16}+4}}$,∴cos∠PQR=2${cos}^{2}\frac{∠PQR}{2}$-1=$\frac{64{-T}^{2}}{64{+T}^{2}}$.
∵$\overrightarrow{PQ}$•$\overrightarrow{QR}$=PQ•QR•cos(π-∠PQR )=($\frac{{T}^{2}}{16}$+4)•(-$\frac{64{-T}^{2}}{64{+T}^{2}}$ )=$\frac{{π}^{2}}{16}$-4,∴T=π=$\frac{2π}{ω}$,∴ω=2.
再根据五点法作图可得2•$\frac{π}{12}$+φ=$\frac{π}{2}$,∴φ=$\frac{π}{3}$,f(x)=2sin(2x+$\frac{π}{3}$).
把函数y=2sinx图象上所有的点横坐标缩短到原来的$\frac{1}{2}$倍,纵坐标不变,可得函数y=2sin2x图象;
再向左平移$\frac{π}{6}$个单位,可得函数y=2sin2(x+$\frac{π}{6}$)=2sin(2x+$\frac{π}{3}$)的图象,
故选:B.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,利用直角三角形中的边角关系、余弦定理求出周期T,再由周期求出ω,由五点法作图求出φ的值,可得f(x)的解析式,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点A,B,C是椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的三个顶点,D是OA的中点,P、Q是直线x=4上的两个动点.
如图,点A,B,C是椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的三个顶点,D是OA的中点,P、Q是直线x=4上的两个动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-∞,0]∪[2,+∞) | C. | (3,+∞) | D. | (-∞,-2]∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
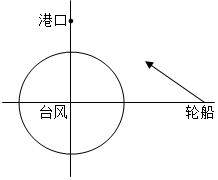 一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西60km处,受影响的范围是半径长为20km的圆形区域.已知港口位于台风中心正北30km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西60km处,受影响的范围是半径长为20km的圆形区域.已知港口位于台风中心正北30km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com