
分析 (Ⅰ)求出原函数的导函数,由已知可得f′(1)=1,f(1)=3,联立方程组求得a,b的值;
(Ⅱ)把a,b的值代入f(x),由导函数的零点把函数的定义域分段,由导函数的符号得到原函数的单调性,利用单调性求得最值.
解答 解:(Ⅰ)f′(x)=3x2-4ax+b,…(2分)
∵f(x)在P(1,3)处的切线为y=x+2,
∴$\left\{\begin{array}{l}{f′(1)=3-4a+b=1}\\{f(1)=1-2a+b=3}\end{array}\right.$,…(4分)
解得:a=2,b=6;…(6分)
(Ⅱ)由(Ⅰ)知f′(x)=3${x}^{2}-8x+6=3(x-\frac{4}{3})^{2}+\frac{2}{3}$,
f′(x)在[-1,4]上恒大于0,从而f(x)在[-1,4]上单调递增.…(10分)
∴f(x)min=f(-1)=-11,f(x)max=f(4)=24.
∴f(x)的值域为[-11,24].…(12分)
点评 本题考查利用导数研究过曲线上某点处的切线方程,曲线在某点处的切线的斜率,就是函数在该点处的导数值,训练了利用导数求函数的最值,是中档题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\int_{\;\;0}^{\;\;1}$xdx | B. | $\int_{\;\;0}^{\;\;1}{{e^x}$dx | C. | $\int_{\;\;0}^{\;\;\frac{π}{2}}$1dx | D. | $\int_{\;\;0}^{\;\;\frac{π}{2}}$cosxdx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f({m}^{n})}{{m}^{n}}$ | B. | logmn•f(lognm) | C. | $\frac{f({n}^{m})}{{n}^{m}}$ | D. | lognm•f(logmn) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
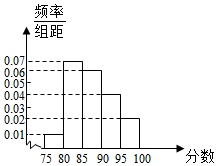 某重点高中拟把学校打造成新兴示范高中,为此制定了很多新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问题5分,调查结束后,按成绩分成5组;第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100),绘制成如图所示的频率分布直方图,已知甲、乙两人同在第3组,丙、丁二人同在第4,5组,现在用分层抽样的方法在第3,4,5组共选取6人进行强化培训.
某重点高中拟把学校打造成新兴示范高中,为此制定了很多新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问题5分,调查结束后,按成绩分成5组;第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100),绘制成如图所示的频率分布直方图,已知甲、乙两人同在第3组,丙、丁二人同在第4,5组,现在用分层抽样的方法在第3,4,5组共选取6人进行强化培训.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
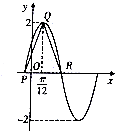 函数f(x)=2sin(ωx+φ)(?>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图所示.,若$\overrightarrow{PQ}$•$\overrightarrow{QR}$=$\frac{{π}^{2}}{16}$-4,为了得到函数f(x)的图象只要把函数y=2sinx图象上所有的点( )
函数f(x)=2sin(ωx+φ)(?>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的图象如图所示.,若$\overrightarrow{PQ}$•$\overrightarrow{QR}$=$\frac{{π}^{2}}{16}$-4,为了得到函数f(x)的图象只要把函数y=2sinx图象上所有的点( )| A. | 横坐标缩短到原来的$\frac{1}{2}$倍,纵坐标不变,再向左平移$\frac{π}{3}$个单位 | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$倍,纵坐标不变,再向左平移$\frac{π}{6}$个单位 | |
| C. | 横坐标伸长到原来的2倍,纵坐标不变,再向左平移$\frac{π}{3}$个单位 | |
| D. | 横坐标伸长到原来的2倍,纵坐标不变,再向左平移$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com