
分析 函数f(x)=($\frac{1}{2}$)x2+4x+3=$(\frac{1}{2})^{(x+2)^{2}-1}$,利用复合函数、指数函数与二次函数的单调性可得最大值.g(x)=x+$\frac{1}{x}$+t,g′(x)=1-$\frac{1}{{x}^{2}}$=$\frac{{x}^{2}-1}{{x}^{2}}$,利用导数研究其单调性即可得出最大值.根据?x1∈R,?x2∈[1,3],使得f(x1)≤g(x2),可得g(x)max≥f(x)max,即可得出.
解答 解:函数f(x)=($\frac{1}{2}$)x2+4x+3=$(\frac{1}{2})^{(x+2)^{2}-1}$,
∵x∈R,∴u(x)=(x+2)2-1≥-1,
∴f(x)∈(0,2].
∵g(x)=x+$\frac{1}{x}$+t,g′(x)=1-$\frac{1}{{x}^{2}}$=$\frac{{x}^{2}-1}{{x}^{2}}$,
∴当x∈[1,3]时,g′(x)≥0,
∴函数g(x)在x∈[1,3]时的单调递增,∴g(x)max=g(3)=$\frac{10}{3}$+t.
?x1∈R,?x2∈[1,3],使得f(x1)≤g(x2),
∴g(x)max≥f(x)max,∴$\frac{10}{3}$+t≥2,解得$t≥-\frac{4}{3}$.
则实数t的取值范围是$[-\frac{4}{3},+∞)$.
故答案为:$[-\frac{4}{3},+∞)$.
点评 本题考查了指数函数与二次函数的单调性、利用导数研究其单调性极值与最值、不等式的解法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
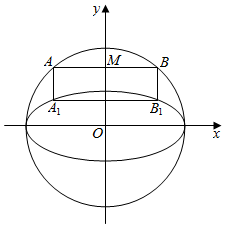 在平面直角坐标系xOy中,已知圆O:x2+y2=4和椭圆C:$\frac{{x}^{2}}{4}$+y2=1,动直线l过点M(0,$\frac{3}{2}$)且与圆O交于A,B两点,自A,B分别作x轴的垂线交椭圆C于A1,B1,A1与A,B1与B不在x轴的异侧.
在平面直角坐标系xOy中,已知圆O:x2+y2=4和椭圆C:$\frac{{x}^{2}}{4}$+y2=1,动直线l过点M(0,$\frac{3}{2}$)且与圆O交于A,B两点,自A,B分别作x轴的垂线交椭圆C于A1,B1,A1与A,B1与B不在x轴的异侧.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3n+1 | B. | 3n | C. | n | D. | n-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com